
ЁОЬтФПЁПЁАЖЫЮчНкЁБЪЧЮвЙњЕФДЋЭГМбНкЃЌУёМфРњРДгаГдЁАєезгЁБЕФЯАЫзЃЎЮвЪаФГЪГЦЗГЇЮЊСЫНтЪаУёЖдШЅФъЯњСПНЯКУЕФШтЯкєеЁЂЖЙЩГЯкєеЁЂКьдцЯкєеЁЂЕАЛЦЯкєеЃЈвдЯТЗжБ№гУAЃЌBЃЌCЃЌDБэЪОЃЉетЫФжжВЛЭЌПкЮЖєезгЕФЯВАЎЧщПіЃЌдкНкЧАЖдФГОгУёЧјЪаУёНјааСЫГщбљЕїВщЃЌВЂНЋЕїВщЧщПіЛцжЦГЩШчЯТСНЗљЭГМЦЭМЃЈЩаВЛЭъећЃЉЃЎ
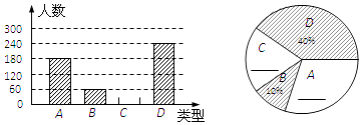
ЧыИљОнвдЩЯаХЯЂЛиД№ЃК
ЃЈ1ЃЉНЋСНЗљВЛЭъећЕФЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉБОДЮВЮМгГщбљЕїВщЕФОгУёгаЖрЩйШЫЃП
ЃЈ3ЃЉШєОгУёЧјга8000ШЫЃЌЧыЙРМЦАЎГдDєеЕФШЫЪ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉ600ШЫЃЛЃЈ3ЃЉ3200ШЫ
ЁОНтЮіЁП
ЃЈ1ЃЉЧѓГіCРрЕФШЫЪ§ЃЈзмШЫЪ§МѕШЅЦфЫќИїзщЕФШЫЪ§ЃЉЃЛЧѓГіCРрЁЂAРрЫљеМЕФАйЗжЪ§ЃЌЛГіЭМаЮПЩЕУЃЛ
ЃЈ2ЃЉРћгУзмШЫЪ§=BРрЕФШЫЪ§ЁТЦфЫљеМЕФАйЗжБШПЩЧѓЕУЃЛ
ЃЈ3ЃЉРћгУ8000ГЫвдЖдгІЕФАйЗжБШПЩЧѓЕУЃЎ
ЃЈ1ЃЉБОДЮВЮМгГщбљЕїВщЕФОгУёЕФШЫЪ§ЪЧЃК60ЁТ10%=600ЃЈШЫЃЉ
ЁрCРрЕФШЫЪ§ЪЧЃК600Љ180Љ60Љ240=120ЃЈШЫЃЉЃЌЫљеМЕФАйЗжБШЪЧЃК![]() ЁС100%=20%ЃЌ
ЁС100%=20%ЃЌ
ЙЪAРрЫљеМЕФАйЗжБШЪЧЃК![]() ЁС100%=30%ЃЎ
ЁС100%=30%ЃЎ
ШчЭМЃЌВЙШЋЭГМЦЭМШчЯТЃК
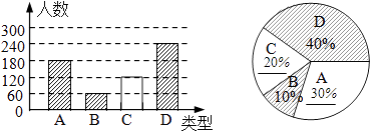
ЃЈ2ЃЉгЩЃЈ1ЃЉПЩЕУБОДЮВЮМгГщбљЕїВщЕФОгУёЕФШЫЪ§ЪЧ600ЃЈШЫЃЉ
Д№ЃКБОДЮВЮМгГщбљЕїВщЕФОгУёга600ШЫЃЛ
ЃЈ3ЃЉНтЃК8000ЁС40%=3200ЃЈШЫЃЉ
Д№ЃКЙРМЦАЎГдDєеЕФШЫЪ§га3200ШЫЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
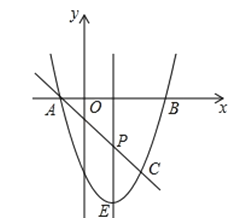
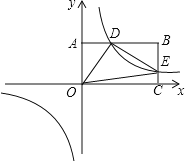
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ax2+bxЉ3гыxжсНЛгкAЃЌBСНЕуЃЈAЕудкBЕузѓВрЃЉЃЌAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌжБЯпlгыХзЮяЯпНЛгкAЃЌCСНЕуЃЌЦфжаCЕуЕФКсзјБъЮЊ2ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉPЪЧЯпЖЮACЩЯЕФвЛИіЖЏЕуЃЌЙ§PЕузїyжсЕФЦНааЯпНЛХзЮяЯпгкEЕуЃЌЧѓЯпЖЮPEГЄЖШЕФзюДѓжЕЃЛ
ЃЈ3ЃЉЕуGЪЧХзЮяЯпЩЯЕФЖЏЕуЃЌдкxжсЩЯЪЧЗёДцдкЕуFЃЌЪЙAЃЌCЃЌFЃЌGетбљЕФЫФИіЕуЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШчЙћДцдкЃЌЧѓГіЫљгаТњзуЬѕМўЕФFЕузјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
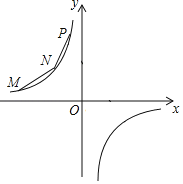
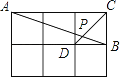
ЁОЬтФПЁПШчЭМЫљЪОЃЌMЁЂNЁЂPдкЕкЖўЯѓЯоЃЌКсзјБъЗжБ№ЪЧЉ4ЁЂЉ2ЁЂЉ1ЃЌЫЋЧњЯпyЃН![]() Й§MЁЂNЁЂPШ§ЕуЃЌЧвMNЃНNPЃЎ
Й§MЁЂNЁЂPШ§ЕуЃЌЧвMNЃНNPЃЎ
ЃЈ1ЃЉЧѓЫЋЧњЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЙ§PЕуЕФжБЯпlНЛxжсгкAЃЌНЛyжсгкBЃЌЧвPAЃН4ABЃЌЧвНЛyЃН![]() гкСэвЛЕуQЃЌЧѓQЕузјБъЃЛ
гкСэвЛЕуQЃЌЧѓQЕузјБъЃЛ
ЃЈ3ЃЉвдPNЮЊБпЃЈЫГЪБеыЗНЯђЃЉзїе§ЗНаЮPNEFЃЌЦНвЦе§ЗНаЮЪЙNТфдкxжсЩЯЃЌЕуPЁЂEЖдгІЕФЕуPЁфЁЂE'е§КУТфдкЗДБШР§КЏЪ§yЃН![]() ЩЯЃЌЧѓFЖдгІЕуFЁфЕФзјБъЃЎ
ЩЯЃЌЧѓFЖдгІЕуFЁфЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЗДБШР§КЏЪ§![]() ЃЈkЃО0ЃЉгыГЄЗНаЮOABCдкЕквЛЯѓЯоЯрНЛгкDЃЌEСНЕуЃЌOA=2ЃЌOC=4ЃЌСЌНсODЁЂOEЁЂDEЃЎМЧЁїOADЁЂЁїOCEЕФУцЛ§ЗжБ№ЮЊ
ЃЈkЃО0ЃЉгыГЄЗНаЮOABCдкЕквЛЯѓЯоЯрНЛгкDЃЌEСНЕуЃЌOA=2ЃЌOC=4ЃЌСЌНсODЁЂOEЁЂDEЃЎМЧЁїOADЁЂЁїOCEЕФУцЛ§ЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЃЎЕБ
ЃЎЕБ![]() =2ЪБЃЌЧѓkЕФжЕМАЕуDЁЂEЕФзјБъЃЌЪдХаЖЯЁїODEЕФаЮзДЃЎ
=2ЪБЃЌЧѓkЕФжЕМАЕуDЁЂEЕФзјБъЃЌЪдХаЖЯЁїODEЕФаЮзДЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЯрЭЌЕФаЁе§ЗНаЮзщГЩЕФЭјИёжаЃЌЕуAЁЂBЁЂCЁЂDЖМдкетаЉаЁе§ЗНаЮЕФЖЅЕуЩЯЃЌABЁЂCDЯрНЛгкЕуPЃЌдђtanЁЯAPDЕФжЕЪЧ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌвбжЊОиаЮABCDЃЌAB=4ЃЌAD=3ЃЌЕуEЮЊБпDCЩЯВЛгыЖЫЕужиКЯЕФвЛИіЖЏЕуЃЌСЌНгBEЃЌНЋBCEбиBEЗелЕУЕНBEFЃЌСЌНгAFВЂбгГЄНЛCDгкЕуGЃЌдђЯпЖЮCGЕФзюДѓжЕЪЧ( )
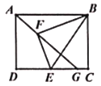
A.1B.1.5C.4-![]() D.4-
D.4-![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧФГАрМзЁЂввЁЂБћШ§ЮЛЭЌбЇзюНќ5ДЮЪ§бЇГЩМЈМАЦфЫљдкАрМЖЯргІЦНОљЗжЕФелЯпЭГМЦЭМЃЌдђЯТСаХаЖЯДэЮѓЕФЪЧ( ).

A. МзЕФЪ§бЇГЩМЈИпгкАрМЖЦНОљЗжЃЌЧвГЩМЈБШНЯЮШЖЈ
B. ввЕФЪ§бЇГЩМЈдкАрМЖЦНОљЗжИННќВЈЖЏЃЌЧвБШБћКУ
C. БћЕФЪ§бЇГЩМЈЕЭгкАрМЖЦНОљЗжЃЌЕЋГЩМЈж№ДЮЬсИп
D. ОЭМзЁЂввЁЂБћШ§ИіШЫЖјбдЃЌввЕФЪ§бЇГЩМЈзюВЛЮШ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкСтаЮABCDжаЃЌЖдНЧЯп![]() ЯрНЛгкЕуMЃЌвбжЊ
ЯрНЛгкЕуMЃЌвбжЊ![]() ЃЌЕуEдкЩфЯп
ЃЌЕуEдкЩфЯп![]() ЩЯЃЌ
ЩЯЃЌ![]() ЃЌЕуPДгЕуBГіЗЂЃЌвдУПУы
ЃЌЕуPДгЕуBГіЗЂЃЌвдУПУы![]() ИіЕЅЮЛЕФЫйЖШбиBDЗНЯђЯђжеЕуDдШЫйдЫЖЏЃЌЙ§Еу
ИіЕЅЮЛЕФЫйЖШбиBDЗНЯђЯђжеЕуDдШЫйдЫЖЏЃЌЙ§Еу![]() зї
зї![]() НЛЩфЯп
НЛЩфЯп![]() гкЕу
гкЕу![]() ЃЌвд
ЃЌвд![]() ЮЊСкБпЙЙдьЦНааЫФБпаЮ
ЮЊСкБпЙЙдьЦНааЫФБпаЮ![]() ЃЌЩшЕу
ЃЌЩшЕу![]() ЕФдЫЖЏЪБМфЮЊ
ЕФдЫЖЏЪБМфЮЊ![]() ЃЛ
ЃЛ
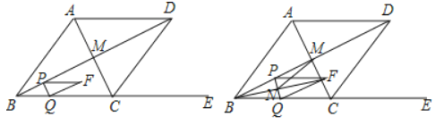
ЃЈ1ЃЉ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓЕу![]() Тфдк
Тфдк![]() ЩЯЪБ
ЩЯЪБ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉЧѓЦНааЫФБпаЮ![]() гы
гы![]() жиЕўВПЗжУцЛ§Sгы
жиЕўВПЗжУцЛ§Sгы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ4ЃЉСЌНгЦНааЫФБпаЮ![]() ЕФЖдНЧЯп
ЕФЖдНЧЯп![]() ЃЌЩш
ЃЌЩш![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЕБ
ЃЌЕБ![]() гы
гы![]() ЕФБпЦНааЃЈВЛжиКЯЃЉЛђДЙжБЪБЃЌжБНгаДГі
ЕФБпЦНааЃЈВЛжиКЯЃЉЛђДЙжБЪБЃЌжБНгаДГі![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌвдЕу
ЃЌвдЕу![]() ЮЊдВаФЃЌвд
ЮЊдВаФЃЌвд![]() ЮЊАыОЖзїгХЛЁ
ЮЊАыОЖзїгХЛЁ![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() .Еу
.Еу![]() дкгХЛЁ
дкгХЛЁ![]() ЩЯДгЕу
ЩЯДгЕу![]() ПЊЪМвЦЖЏЃЌЕНДяЕу
ПЊЪМвЦЖЏЃЌЕНДяЕу![]() ЪБЭЃжЙЃЌСЌНг
ЪБЭЃжЙЃЌСЌНг![]() .
.
ЃЈ1ЃЉЕБ![]() ЪБЃЌХаЖЯ
ЪБЃЌХаЖЯ![]() гыгХЛЁ
гыгХЛЁ![]() ЕФЮЛжУЙиЯЕЃЌВЂМгвджЄУїЃЛ
ЕФЮЛжУЙиЯЕЃЌВЂМгвджЄУїЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓЕу
ЪБЃЌЧѓЕу![]() дкгХЛЁ
дкгХЛЁ![]() ЩЯвЦЖЏЕФТЗЯпГЄМАЯпЖЮ
ЩЯвЦЖЏЕФТЗЯпГЄМАЯпЖЮ![]() ЕФГЄ.
ЕФГЄ.
ЃЈ3ЃЉСЌНг![]() ЃЌЩш
ЃЌЩш![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌжБНгаДГі
ЃЌжБНгаДГі![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
БИгУЭМ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com