
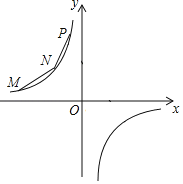
【题目】如图所示,M、N、P在第二象限,横坐标分别是﹣4、﹣2、﹣1,双曲线y=![]() 过M、N、P三点,且MN=NP.
过M、N、P三点,且MN=NP.
(1)求双曲线的解析式;
(2)过P点的直线l交x轴于A,交y轴于B,且PA=4AB,且交y=![]() 于另一点Q,求Q点坐标;
于另一点Q,求Q点坐标;
(3)以PN为边(顺时针方向)作正方形PNEF,平移正方形使N落在x轴上,点P、E对应的点P′、E'正好落在反比例函数y=![]() 上,求F对应点F′的坐标.
上,求F对应点F′的坐标.
【答案】(1)双曲线的解析式为y=﹣![]() ;(2)Q(
;(2)Q(![]() ,﹣5);(3)点F′的坐标为(﹣5,3).
,﹣5);(3)点F′的坐标为(﹣5,3).
【解析】
(1)先表示出点M,N,P的坐标,进而得出MN2,NP2,建立方程求解,即可得出结论;
(2)分点A在x轴的正半轴或负半轴上,判断出△AOB∽∠PQB,得出比例式,即可得出结论;
(3)先确定出点E,F坐标,设出点N'的坐标,进而得出点E',F',P'的坐标,即可得出结论.
(1)∵双曲线y=![]() 过M、N、P三点,
过M、N、P三点,
∴M(﹣4,﹣![]() ),N(﹣2,﹣
),N(﹣2,﹣![]() ),P(﹣1,﹣k),
),P(﹣1,﹣k),
∴MN2=[(﹣4﹣(﹣2)]2+[(﹣![]() )﹣(﹣
)﹣(﹣![]() )]2=4+
)]2=4+![]() ,NP2=1+
,NP2=1+![]() ,
,
∵MN=NP,
∴MN2=NP2,
∴4+![]() =1+
=1+![]() ,
,
∴k=﹣4或k=4(由于点P在第二象限,不符合题意,舍去),
∴双曲线的解析式为y=﹣![]() ;
;
(2)由(1)知,双曲线的解析式为y=﹣![]() ①,
①,
由(1)知,k=﹣4,
∴P(﹣1,4),
如图1,过点P作PQ⊥y轴于Q,则PQ=1,
Ⅰ、当点A在x轴正半轴时,
∵PA=4AB,
∴PB=3AB,
∵PQ⊥y轴,OA⊥y轴,
∴OA∥PQ,
∴△AOB∽∠PQB,
∴![]() ,
,
∴![]() =
=![]() ,
,
∴OA=![]() ,
,
∴A(![]() ,0),
,0),
∵P(﹣1,4),
∴直线PA的解析式为y=﹣3x+1②,
联立①②解得,![]() 或
或 ,
,
∴Q(![]() ,﹣3),
,﹣3),
Ⅱ、当点A在x轴负半轴上,
∵PA'=A'B',
∴PB'=5A'B',
同(Ⅰ)的方法得,△A'OB'∽△PQB',
∴![]() ,
,
∴![]() ,
,
∴OA'=![]() ,
,
∴A'(﹣![]() ,0),
,0),
∴直线PA'的解析式为y=﹣5x﹣1③,
联立①③解得,![]() 或
或 ,
,
∴Q(![]() ,﹣5);
,﹣5);
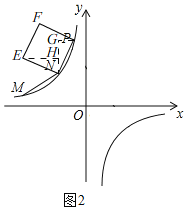
(3)如图2,由(1)知,k=﹣4,
∴P(﹣1,4),N(﹣2,2),
∵四边形PNEF是正方形,
∴EN=PN,∠PNE=90°,
过点N作y轴的平行线交过点P作x轴的平行线于G,过点E作EH⊥NG于H,
∴∠EHN=∠NGP=90°,
∴∠HEN+∠ENH=90°,∠ENH+∠PNG=90°,
∴∠HEN=∠GNP,
∴△EHN≌△NGP(AAS),
∴NH=PG=|﹣2﹣(﹣1)|=1,EH=NG=|4﹣2|=2,
∴E(﹣4,3),
同理:F(﹣3,5),
记点N平移到x轴的N'位置,设N'(m,0),
∵N(﹣1,4),
∴点N向左平移(﹣2﹣m)个单位,再向下平移2个单位,
∴点P,E,F也向左平移(﹣2﹣m)个单位,再向下平移2个单位,得到点P'(m+1,2),E'(m﹣2,1),F'(m﹣1,3),
∴点P′、E'正好落在反比例函数y=![]() 上,
上,
∴b=2(m+1)=m﹣2,
∴m=﹣4,
∴F'(﹣5,3),
即F对应点F′的坐标为(﹣5,3).



 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
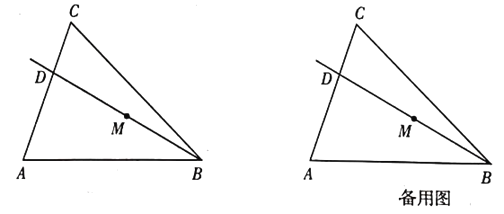
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,射线
,射线![]() 从与射线
从与射线![]() 重合的位置开始,绕点
重合的位置开始,绕点![]() 按顺时针方向旋转,与射线
按顺时针方向旋转,与射线![]() 重合时就停止旋转,射线
重合时就停止旋转,射线![]() 与线段
与线段![]() 相交于点
相交于点![]() ,点
,点![]() 是线段
是线段![]() 的中点.
的中点.
(1)求线段![]() 的长;
的长;
(2)①当点![]() 与点
与点![]() 、点
、点![]() 不重合时,过点
不重合时,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,在射线
,在射线![]() 旋转的过程中,
旋转的过程中,![]() 的大小是否发生变化?若不变,求
的大小是否发生变化?若不变,求![]() 的度数;若变化,请说明理由.
的度数;若变化,请说明理由.
②在①的条件下,连接![]() ,直接写出
,直接写出![]() 面积的最小值____________.
面积的最小值____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )
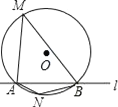
A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物业公司计划对所管理的小区3000m2区域进行绿化,经投标由甲、乙两个工程队来完成,甲、乙两个工程队每天共完成绿化面积150m2,甲队完成600m2区域的绿化面积与乙队完成300m2区域的绿化面积所用的天数相同.
(1)求甲、乙两个工程队每天各能完成多少面积的绿化?
(2)若甲队每天绿化费用是0.6万元,乙队每天绿化费用是0.2万元,该物业公司要使这次绿化总费用不超过17万元,则至少安排乙工程队绿化多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近期,某国遭遇了近年来最大的经济危机,导致该国股市大幅震荡,昨天某支股票累计卖出的数量和交易时间之间的关系如图中虚线所示,累计买入的数量和交易时间之间的关系如图中实线所示,其中点A是实线和虚线的交点,点C是BE的中点,CD与横轴平行,则下列关于昨天该股票描述正确的是( )
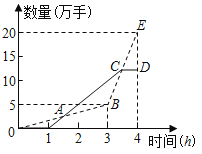
A.交易时间在3.5h时累计卖出的数量为12万手
B.交易时间在1.4h时累计卖出和累计买入的数量相等
C.累计卖出的数量和累计买入的数量相差1万手的时刻有5个
D.从点A对应的时刻到点C对应的时刻,平均每小时累计卖出的数量小于买入的数量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1的解析式为![]() ,直线l2的解析式为
,直线l2的解析式为![]() ,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
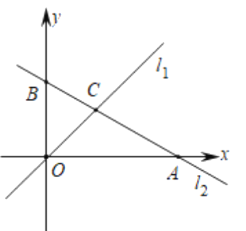

(1)求点A、点B、点C的坐标,并求出△COB的面积;
(2)若直线l2上存在点P(不与B重合),满足S△COP=S△COB,请求出点P的坐标;
(3)在y轴右侧有一动直线平行于y轴,分别与l1,l2交于点M、N,且点M在点N的下方,y轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2﹣9(其中a>0)上,AB∥x轴,点P是抛物线的顶点,tan∠PBA=2,∠BAC=45°.
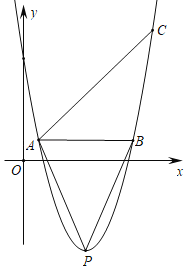
(1)填空:抛物线的顶点P的坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为10,当2m﹣3≤x≤2m+5时,y的最小值为5,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A,B,C,D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
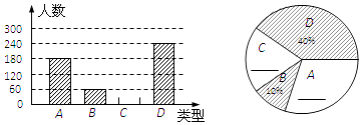
请根据以上信息回答:
(1)将两幅不完整的图补充完整;
(2)本次参加抽样调查的居民有多少人?
(3)若居民区有8000人,请估计爱吃D粽的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小桥用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成,按照这样的规律排列下去,则第9个图案中共有( )和黑子.
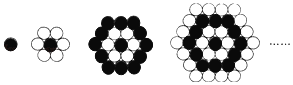
A.37B.42C.73D.121
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com