
【题目】如图,在平面直角坐标系![]() 中,与y轴相切的
中,与y轴相切的![]() 与x轴交于A、B两点,AC为
与x轴交于A、B两点,AC为![]() 直径,
直径,![]() ,
,![]() ,连结BC,点P为劣弧
,连结BC,点P为劣弧![]() 上点,点Q为线段AB上点,且
上点,点Q为线段AB上点,且![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,则当 NQ平分
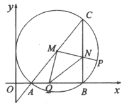
,则当 NQ平分![]() 时,点P坐标是________.
时,点P坐标是________.
【答案】(![]() ,
,![]() )
)
【解析】
作MK⊥AB,ME⊥BC,PF⊥MK,求证出![]() ,
,![]() ,再证明△QMN
,再证明△QMN![]() △QBN,证明出并设MN=BN=x,则EN=4-x,求出x,再证明出△EMN
△QBN,证明出并设MN=BN=x,则EN=4-x,求出x,再证明出△EMN![]() △PMF,
△PMF,
利用相似求出FK=MK-MF=4-![]() =
=![]() ,OK+PF=5+
,OK+PF=5+![]() =
=![]() ,即可求出坐标.
,即可求出坐标.
如图:作MK⊥AB,ME⊥BC,PF⊥MK,

∵ME⊥BC,AB⊥BC,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() 直径,
直径,![]() ,
,![]() ,
,
∴BC=8,
同理:![]() ,
,
∵![]() ,
,
∴∠QMN=∠NBQ=90°,
∵NQ平分![]() ,
,
∴QM=QB,
∴△QMN![]() △QBN,
△QBN,
∴MN=BN,
∵ME⊥BC,
∴![]() ,
,
设MN=BN=x,则EN=4-x,
∵![]() ,
,
∴![]() ,
,
解得x=![]() ,
,
∴MN=BN=![]() ,则EN=
,则EN=![]() ,
,
又PF⊥MK,ME⊥BC,
∴△EMN![]() △PMF,
△PMF,
∴![]() ,
,![]()
∵MP=5,
∴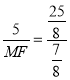 ,
,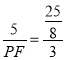
解得MF=![]() ,PF=
,PF=![]() ,
,
∴FK=MK-MF=4-![]() =
=![]() ,OK+PF=5+
,OK+PF=5+![]() =
=![]() ,
,
即P点纵坐标为![]() ,横坐标为
,横坐标为![]() ,
,
即P点坐标为(![]() ,
,![]() ).
).
故答案为:(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
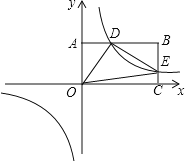
【题目】如图,反比例函数![]() (k>0)与长方形OABC在第一象限相交于D,E两点,OA=2,OC=4,连结OD、OE、DE.记△OAD、△OCE的面积分别为
(k>0)与长方形OABC在第一象限相交于D,E两点,OA=2,OC=4,连结OD、OE、DE.记△OAD、△OCE的面积分别为![]() 、
、![]() .当
.当![]() =2时,求k的值及点D、E的坐标,试判断△ODE的形状.
=2时,求k的值及点D、E的坐标,试判断△ODE的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
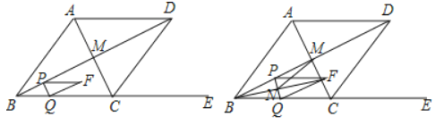
【题目】如图,在菱形ABCD中,对角线![]() 相交于点M,已知
相交于点M,已知![]() ,点E在射线
,点E在射线![]() 上,
上,![]() ,点P从点B出发,以每秒
,点P从点B出发,以每秒![]() 个单位的速度沿BD方向向终点D匀速运动,过点
个单位的速度沿BD方向向终点D匀速运动,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,以
,以![]() 为邻边构造平行四边形
为邻边构造平行四边形![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() ;
;
(1)![]() ;
;
(2)求点![]() 落在
落在![]() 上时
上时![]() 的值;
的值;
(3)求平行四边形![]() 与
与![]() 重叠部分面积S与
重叠部分面积S与![]() 之间的函数关系式;
之间的函数关系式;
(4)连接平行四边形![]() 的对角线
的对角线![]() ,设
,设![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,当
,当![]() 与
与![]() 的边平行(不重合)或垂直时,直接写出
的边平行(不重合)或垂直时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EF⊥AE,过点A作AF∥BC,且AF、EF相交于点F.

(1)求证:∠C=∠BAD;
(2)求证:AC=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
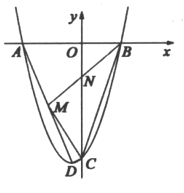
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与x轴交于
与x轴交于![]() 、B两点,与y轴交点C的坐标为
、B两点,与y轴交点C的坐标为![]() ,
,![]() 为抛物线顶点,连结AD,点M为线段AD上动点(不含端点),BM与y轴交于点N.
为抛物线顶点,连结AD,点M为线段AD上动点(不含端点),BM与y轴交于点N.
(1)求抛物线解析式;
(2)是否存在点M使得![]() 与
与![]() 相似,若存在请求出点M的坐标,若不存在,请说明理由;
相似,若存在请求出点M的坐标,若不存在,请说明理由;
(3)求当BM将四边形ABCM分为面积相等的两部分时ON的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
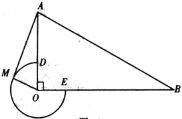
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 为半径作优弧
为半径作优弧![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .点
.点![]() 在优弧
在优弧![]() 上从点
上从点![]() 开始移动,到达点
开始移动,到达点![]() 时停止,连接
时停止,连接![]() .
.
(1)当![]() 时,判断
时,判断![]() 与优弧
与优弧![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)当![]() 时,求点
时,求点![]() 在优弧
在优弧![]() 上移动的路线长及线段
上移动的路线长及线段![]() 的长.
的长.
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
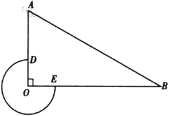
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近日,崂山区教体局对参加2018年崂山区禁毒知识竞赛的2500名初中学生的初试成绩(成绩均为整数)进行一次抽样调查,所得数据如下表:
成绩分组 | 60.5~70.5 | 70.5~80.5 | 80.5~90.5 | 90.5~100.5 |
频数 | 50 | 150 | 200 | 100 |
(1)抽取样本的总人数;
(2)根据表中数据,补全图中频数分布直方图;
(3)若规定初试成绩在90分以上(不包括90分)的学生进入决赛,则全区进入决赛的初中学生约有多少人.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com