
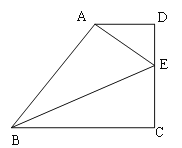
【题目】如图,在梯形![]() 中,
中,![]() ∥
∥![]() ,∠
,∠![]() =90°,
=90°,![]() ,
,![]()
⑴求![]() 的长;
的长;
⑵若∠![]() 的平分线交
的平分线交![]() 于点
于点![]() ,连结
,连结![]() ,求∠
,求∠![]() 的正切值.
的正切值.
【答案】(1)4;(2)2
【解析】
(1) 过点A作AFBC垂足为F,得到BF的长度,在Rt△AFB中运用勾股定理即可得到AF的长度,利用AF=DC进而得到答案;
(2)先证明![]() ≌
≌![]() (SAS),根据全等三角形的性质得到∠AEB=∠CEB,运用勾股定理求解CE的长度即可得到答案;
(SAS),根据全等三角形的性质得到∠AEB=∠CEB,运用勾股定理求解CE的长度即可得到答案;
解:(1)过点A作AFBC垂足为F,
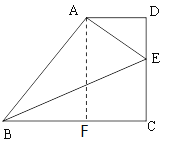
由题意得FC=AD=2,AF=CD,.
∵BC=5,
∴BF=5-2=3,
在Rt△AFB中:
![]() (勾股定理),
(勾股定理),
即:![]()
解得AF=4,
∴CD=4;
(2)由AB=BC,∠ABE=∠CBE,BE=BE,
得到![]() ≌
≌![]() (SAS),
(SAS),
∴∠AEB=∠CEB(全等三角形对应边相等),
∴AE=EC(全等三角形对应边相等),
设AE=EC=![]() ,
,
则DE=![]() ,
,
在Rt△ADE中,
![]()
![]() ,
,
解得![]() ,
,



 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案科目:初中数学 来源: 题型:
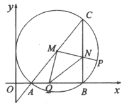
【题目】如图,在平面直角坐标系![]() 中,与y轴相切的
中,与y轴相切的![]() 与x轴交于A、B两点,AC为
与x轴交于A、B两点,AC为![]() 直径,
直径,![]() ,
,![]() ,连结BC,点P为劣弧
,连结BC,点P为劣弧![]() 上点,点Q为线段AB上点,且
上点,点Q为线段AB上点,且![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,则当 NQ平分
,则当 NQ平分![]() 时,点P坐标是________.
时,点P坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
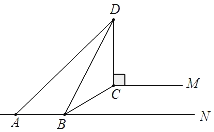
【题目】如图,BC是坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是45°和60°.
(1)求灯杆CD的高度;
(2)求AB的长度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了满足师生的阅读需求,某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册.
(1)求这两年藏书的年均增长率;
(2)经统计知:中外古典名著的册数在2016年底仅占当时藏书总量的5.6%,在这两年新增加的图书中,中外古典名著所占的百分率恰好等于这两年藏书的年均增长率,那么到2018年底中外古典名著的册数占藏书总量的百分之几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织了一次体育测试,测试项目有A“立定跳远”、B“掷实心球”、C“仰卧起坐”、D“100米跑”、E“800米跑”.规定:每名学生测试三项,其中A、B为必测项目,第三项在C、D、E中随机抽取,每项10分(成绩均为整数且不低于0分).
(1)完成A、B必测项目后,用列表法,求甲、乙两同学第三项抽取不同项目的概率;
(2)某班有6名男生抽到了E“800米跑”项目,他们的成绩分别(单位:分)为:x,6,7,8,8,9.
①已知这组成绩的平均数和中位数相等,且x不是这组成绩中最高的,则x= ;
②该班学生丙因病错过了测试,补测抽到了E“800米跑”项目,加上丙同学的成绩后,发现这组成绩的众数与中位数相等,但平均数比原来的平均数小,则丙同学“800米跑”的成绩为多少?;
甲 乙 | |||
查看答案和解析>>
科目:初中数学 来源: 题型:
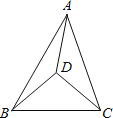
【题目】如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC=_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个矩形纸片![]() ,将该纸片放置在平面直角坐标系中,点
,将该纸片放置在平面直角坐标系中,点![]() ,点
,点![]() ,点P为
,点P为![]() 边上的动点.
边上的动点.
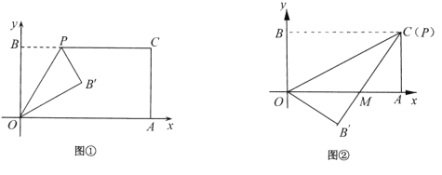
(1)如图①,经过点O、P折叠该纸片,得点![]() 和折痕
和折痕![]() .当点P的坐标为
.当点P的坐标为![]() 时,求
时,求![]() 的度数;
的度数;
(2)如图②,当点P与点C重合时,经过点O、P折叠纸片,使点B落在点![]() 的位置,
的位置,![]() 与
与![]() 交于点M,求点M的坐标;
交于点M,求点M的坐标;
(3)过点P作直线![]() ,交
,交![]() 于点Q,再取
于点Q,再取![]() 中点T,
中点T,![]() 中点N,分别以
中点N,分别以![]() ,
,![]() ,
,![]() ,
,![]() 为折痕,依次折叠该纸片,折叠后点O的对应点与点B的对应点恰好重合,且落在线段
为折痕,依次折叠该纸片,折叠后点O的对应点与点B的对应点恰好重合,且落在线段![]() 上,A、C的对应点也恰好重合,也落在线段
上,A、C的对应点也恰好重合,也落在线段![]() 上,求此时点P的坐标(直接写出结果即可).
上,求此时点P的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在绿化某县城与高速公路的连接路段中,需购买罗汉松、雪松两种树苗共400株,罗汉松树苗每株60元,雪松树苗每株70元.相关资料表明:罗汉松、雪松树苗的成活率分别为70%,90%.
(1)若购买这两种树苗共用去26500元,则罗汉松、雪松树苗各购买多少株?
(2)绿化工程来年一般都要将死树补上新苗,现要使该两种树苗来年共补苗不多于80株,则罗汉松树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,才能使购买树苗的费用最低?请求出最低费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com