
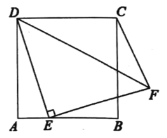
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,点
,点![]() 是
是![]() 边上-动点,连接
边上-动点,连接![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() ,连接
,连接![]() ,则
,则![]() 的最小值是( )
的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
连接BF,过点F作FG⊥AB交AB延长线于点G,通过证明△AED≌△GFE(AAS),确定F点在BF的射线上运动;作点C关于BF的对称点C',由三角形全等得到∠CBF=45°,从而确定C'点在AB的延长线上;当D、F、C'三点共线时,DF+CF=DC'最小,在Rt△ADC'中,AD=3,AC'=6,求出DC'=![]() 即可.
即可.
解:连接BF,过点F作FG⊥AB交AB延长线于点G,
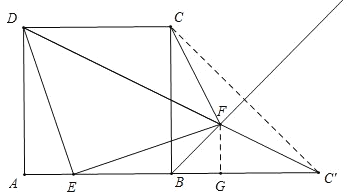
∵将ED绕点E顺时针旋转90°到EF,
∴EF⊥DE,且EF=DE,
∴△AED≌△GFE(AAS),
∴FG=AE,
∴F点在BF的射线上运动,
作点C关于BF的对称点C',
∵EG=DA,FG=AE,
∴AE=BG,
∴BG=FG,
∴∠FBG=45°,
∴∠CBF=45°,
∴C'点在AB的延长线上,
当D、F、C'三点共线时,DF+CF=DC'最小,
在Rt△ADC'中,AD=3,AC'=6,
∴DC'=![]() ,
,
∴DF+CF的最小值为![]() ,
,
故选:A.


科目:初中数学 来源: 题型:
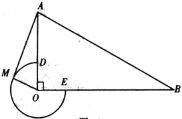
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 为半径作优弧
为半径作优弧![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .点
.点![]() 在优弧
在优弧![]() 上从点
上从点![]() 开始移动,到达点
开始移动,到达点![]() 时停止,连接
时停止,连接![]() .
.
(1)当![]() 时,判断
时,判断![]() 与优弧
与优弧![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)当![]() 时,求点
时,求点![]() 在优弧
在优弧![]() 上移动的路线长及线段
上移动的路线长及线段![]() 的长.
的长.
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
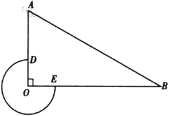
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABDC是⊙O的内接四边形,∠BDC=120°,AB=AC,连接对角线AD,BC,点F在线段BD的延长线上,且CF=DF,⊙O的切线CE交BF于点E.
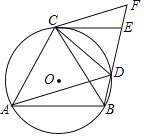
(1)求证:CE∥AB;
(2)求证:AD=BD+CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
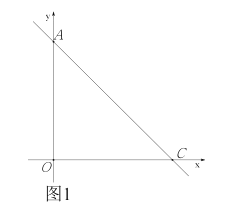
【题目】平面直角坐标系中,直线![]() 交坐标轴于点
交坐标轴于点![]() 、点
、点![]() 且
且![]() 面积为
面积为![]()
![]() 如图1,求
如图1,求![]() 的值;
的值;
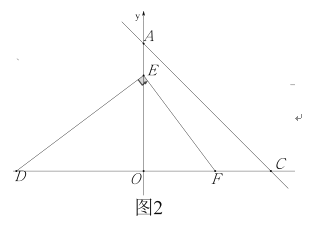
![]() 如图2,点
如图2,点![]() 在
在![]() 轴的负半轴上,
轴的负半轴上,![]() 在线段
在线段![]() 上,连
上,连![]() ,作
,作![]() 交线段
交线段![]() 于
于![]() , 若
, 若![]() 点纵坐标为
点纵坐标为![]() 长度为
长度为![]() ,求
,求![]() 与
与![]() 的函数关系式(不写自变量取值范围);
的函数关系式(不写自变量取值范围);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.
(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为 ;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,抛物线![]() 与线段
与线段![]() 有两个不同的交点,其中点
有两个不同的交点,其中点![]() ,点
,点![]() .有下列结论:
.有下列结论:
①直线![]() 的解析式为
的解析式为![]() ;②方程
;②方程![]() 有两个不相等的实数根;③a的取值范围是
有两个不相等的实数根;③a的取值范围是![]() 或
或![]() .
.
其中,正确结论的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在![]() 中,
中,![]() ,
,![]() , 点
, 点![]() 为
为![]() 中点, 点
中点, 点![]() 在边
在边![]() 上, 连接
上, 连接![]() ,过点
,过点![]() 作
作
![]() 上
上![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 。下列结论:
。下列结论:
(1)![]() (2)
(2)![]() (3)
(3)![]() (4)
(4)![]()
其中正确的是__________(填写所有正确结论的序号)
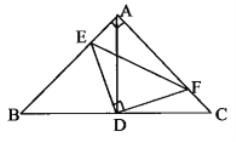
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解朝阳社区![]() 岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
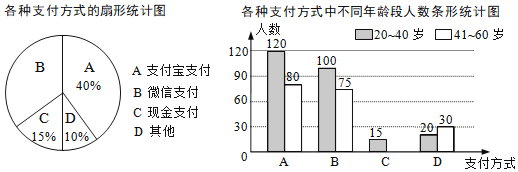
(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中![]() 岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com