
分析 (1)根据两抛物线的关联依次判断即可;
(2)根据两抛物线关联的定义直接列式得出结论;
(3)分当点C位于AD左侧和当点C位于AD右侧,借助关联的意义设出点C坐标,表示出点B坐标代入抛物线解析式即可求出点C坐标.
解答 解:(1)由①知,y=-2(x-1)2+5,
∴抛物线①:y=-2x2+4x+3的顶点坐标为(1,5),
把x=1代入抛物线②:y=2x2+4x-1,得y=5,
∴抛物线①的顶点在抛物线②上,
又由②y=2(x+1)2-3,
∴抛物线②的顶点坐标为(-1,-3),
把x=-1代入抛物线①中,得,y=-3,
∴抛物线②的顶点在抛物线①上,
∴抛物线①与抛物线②关联.
(2)抛物线y=-2x2+4x+3沿x轴翻折后抛物线为y=2x2-4x-3,
即:y=2(x-1)2-5,
设平移后的抛物线解析式为y=2(x-1-m)2-5,
把x=1,y=5代入得2(1-1-m)2-5=5,
∴m=±$\sqrt{5}$,
∵m>0,
∴m=$\sqrt{5}$,
(3)①当点C位于AD左侧时,过点A作AD⊥x轴于D,过点B作BE⊥x轴于E,如图1,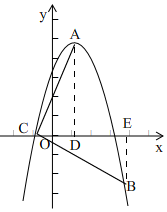
∴△ACD≌△CBE,
∴CE=AD,BE=CD
设C(c,0),
∵点B在x轴下方,
∴点B的纵坐标为c-1;
Ⅰ、当点C在x轴负半轴上时,即:c<0,
∴B(c+5,c-1),
把B(c+5,c-1),代入y=-2(x-1)2+5中得,2c2+17c+26=0,
∴c=-2或c=-$\frac{13}{2}$,
∴C(-2,0)或(-$\frac{13}{2}$,0),
Ⅱ、当点C在x轴正半轴上时,即:0<c<1
把B(5-c,c-1),代入y=-2(x-1)2+5中得,2c2-15c+26=0,
∴c=$\frac{15±\sqrt{17}}{4}$(不符合题意,舍),
②当点C位于AD右侧时,
设C(c,0),同①的方法得出B(c-5,1-c),
将B(c-5,1-c)代入y=-2(x-1)2+5中得,2c2-25c+68=0,
∴c=4或c=$\frac{17}{2}$,
∴C(4,0)或($\frac{17}{2}$,0),
即:点C的坐标为:(-2,0)或(-$\frac{13}{2}$,0)或(4,0)或($\frac{17}{2}$,0).
点评 此题是二次函数综合题,主要考查了新定义,全等三角形的判定和性质,解一元二次方程,分类讨论的思想,理解两抛物线关联是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:填空题
 如图,在平行四边形ABCD中,AC⊥AB,以C为圆心,CA为半径作圆弧交BC于点E,交CD的延长线于点F,以AC上一点O为圆心,OA为半径的圆与BC相切于点G,交AD于点N,若AC=6cm,OA=2cm,则图中阴影部分的面积为 $\frac{23}{3}π-5\sqrt{3}$,cm2(结果不取近似值).
如图,在平行四边形ABCD中,AC⊥AB,以C为圆心,CA为半径作圆弧交BC于点E,交CD的延长线于点F,以AC上一点O为圆心,OA为半径的圆与BC相切于点G,交AD于点N,若AC=6cm,OA=2cm,则图中阴影部分的面积为 $\frac{23}{3}π-5\sqrt{3}$,cm2(结果不取近似值).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AC、BD为圆O的两条垂直的直径,动点P从圆心O出发,沿线段OC-$\widehat{CD}$-线段DO的路线作匀速运动,设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是( )
如图,AC、BD为圆O的两条垂直的直径,动点P从圆心O出发,沿线段OC-$\widehat{CD}$-线段DO的路线作匀速运动,设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是( )| A. | 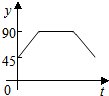 | B. | 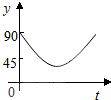 | C. | 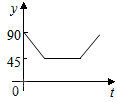 | D. | 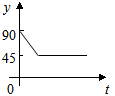 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
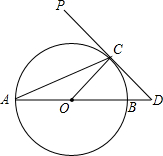 如图,AB是⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且AO=CD,则∠PCA=( )
如图,AB是⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且AO=CD,则∠PCA=( )| A. | 30° | B. | 60° | C. | 67.5° | D. | 45° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线的顶点为A(1,4)、抛物线 与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
如图,已知抛物线的顶点为A(1,4)、抛物线 与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com