
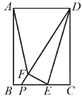
【题目】如图,在矩形ABCD中,AB=6,BC=4,点E是边BC上一动点,把△DCE沿DE折叠得△DFE,射线DF交直线CB于点P,当△AFD为等腰三角形时,DP的长为_____.
【答案】![]() 或
或![]()
【解析】
先根据AD=BC=4,DF=CD=AB=6,得出AD<DF,再分两种情况进行讨论:①当FA=FD时,过F作GH⊥AD与G,交BC于H,根据△DGF∽△PHF,得出![]() ,求得PF的长,进而得出DP的长;②当AF=AD=4时,过F作FH⊥BC于H,交DA的延长线于G,根据勾股定理求得FG,FH的长,再根据△DFG∽△PFH,得出
,求得PF的长,进而得出DP的长;②当AF=AD=4时,过F作FH⊥BC于H,交DA的延长线于G,根据勾股定理求得FG,FH的长,再根据△DFG∽△PFH,得出![]() ,求出PF的长,即可得出PD的长.
,求出PF的长,即可得出PD的长.
∵AD=BC=4,DF=CD=AB=6,∴AD<DF,故分两种情况:
①如图1所示,当FA=FD时,过F作GH⊥AD于G,交BC于H,则HG⊥BC,DG![]() AD=2,∴Rt△DFG中,GF
AD=2,∴Rt△DFG中,GF![]() ,∴FH=6﹣4
,∴FH=6﹣4![]() .
.
∵DG∥PH,
∴△DGF∽△PHF,
∴![]() ,即
,即![]() ,
,
解得:PF![]() 6,
6,
∴DP=DF+PF=6![]() ;
;
②如图2所示,当AF=AD=4时,过F作FH⊥BC于H,交DA的延长线于G,则
Rt△AFG中,AG2+FG2=AF2,即AG2+FG2=16;
Rt△DFG中,DG2+FG2=DF2,即(AG+4)2+FG2=36;
联立两式,解得:FG![]() ,
,
∴FH=6![]() .
.
∵∠G=∠FHP=90°,∠DFG=∠PFH,
∴△DFG∽△PFH,∴![]() ,即
,即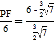 ,
,
解得:PF![]() 6,∴DP=DF+PF=6
6,∴DP=DF+PF=6![]() .
.
故答案为:![]() 或
或![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】某商场以每件30元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数m=162-3x.
(1)写出商场卖这种商品每天的销售利润y(元)与每件的销售价x(元)间的函数关系式;
(2)如果商场要想每天获得最大的销售利润,每件商品的售价定为多少最为合适?最大销售利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() (x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.若四边形ODBE的面积为9,则k的值为( )
(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.若四边形ODBE的面积为9,则k的值为( )
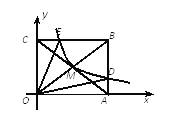
A. 3B. 6C. 9D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
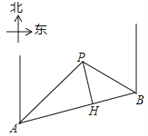
【题目】某条道路上通行车辆限速60千米/时,道路的AB段为监测区,监测点P到AB的距离PH为50米(如图).已知点P在点A的北偏东45°方向上,且在点B的北偏西60°方向上,点B在点A的北偏东75°方向上,那么车辆通过AB段的时间在多少秒以内,可认定为超速?(参考数据:![]() ≈1.7,
≈1.7,![]() ≈1.4).
≈1.4).
查看答案和解析>>
科目:初中数学 来源: 题型:
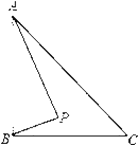
【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.

(1)在旋转过程中,
①当A,D,M三点在同一直线上时,求AM的长.
②当A,D,M三点为同一直角三角形的顶点时,求AM的长.
(2)若摆动臂AD顺时针旋转90°,点D的位置由△ABC外的点D1转到其内的点D2处,连结D1D2,如图2,此时∠AD2C=135°,CD2=60,求BD2的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com