
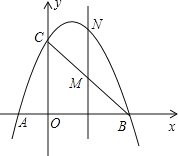
【题目】如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)三点。
(1)求抛物线的解析式。
(2)点M是线段BC上的点(不与B,C重合),过M作MN∥y轴交抛物线于N若点M的横坐标为m,请用m的代数式表示MN的长。
(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由。
【答案】(1)y=﹣x2+2x+3.(2) ﹣m2+3m(0<m<3).(3) 当m=![]() 时,△BNC的面积最大,最大值为
时,△BNC的面积最大,最大值为![]() .
.
【解析】试题分析:(1)利用待定系数法求二次函数的解析式;
(2)先求直线BC的解析式,表示出M、N两点的坐标,利用纵坐标的差计算MN的长即可;
(3)根据面积公式得:S△BNC=S△CMN+S△MNB=![]() |MN||OB|,OB的长是定值为3,所以MN的最大值即为面积的最大值,求MN所表示的二次函数的最值即可.
|MN||OB|,OB的长是定值为3,所以MN的最大值即为面积的最大值,求MN所表示的二次函数的最值即可.
解:(1) ∵抛物线经过点A(1,0),B(3,0),C(0,3)三点,
∴设抛物线的解析式为:y=a(x+1)(x3),
把C(0,3)代入得:3=a(0+1)(03),
a=1,
∴抛物线的解析式:y=-x2+2x+3
(2) 设直线BC的解析式为:y=kx+b,
把B(3,0),C(0,3)代入得: ![]() ,
,
解得:
![]() ,
,
∴直线BC的解析式为y=-x+3,
∴M(m,-m+3),
又∵MN⊥x轴,
∴N(m,-m2+2m+3),
∴MN=(-m2+2m+3)-(-m+3)=-m2+3m(0<m<3)
(3)S△BNC=S△CMN+S△MNB=![]() |MN|·|OB|,
|MN|·|OB|,
∴当|MN|最大时,△BNC的面积最大,
MN=-m2+3m=-(m-![]() )2+
)2+![]() ,
,
所以当m=![]() 时,△BNC的面积最大为
时,△BNC的面积最大为![]() ×
×![]() ×3=
×3=![]()


科目:初中数学 来源: 题型:
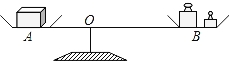
【题目】如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表:
x(cm) | 10 | 15 | 20 | 25 | 30 |
y(g) | 30 | 20 | 15 | 12 | 10 |
(1)猜测y与x之间的函数关系,求出函数关系式并加以验证;
(2)当砝码的质量为24g时,活动托盘B与点O的距离是多少?
(3)将活动托盘B往左移动时,应往活动托盘B中添加还是减少砝码?
查看答案和解析>>
科目:初中数学 来源: 题型:
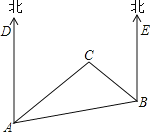
【题目】如图,是A、B、C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西50°方向,从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
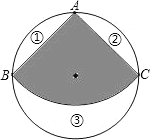
【题目】如图,从一个半径为1的圆形铁皮中剪下一个圆心角为90°的扇形BAC.
(1)求这个扇形的面积;
(2)若将扇形BAC围成一个圆锥的侧面,这个圆锥的底面直径是多少?能否从最大的余料③中剪出一个圆做该圆锥的底面?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车收费标准是:起步价10元,可乘3千米;3千米到5千米,每千米1.3元;超过5千米,每千米2.4元。
(1)若某人乘坐了![]() (
(![]() )千米的路程,则他应支付的费用是多少?
)千米的路程,则他应支付的费用是多少?
(2)若某人乘坐的路程为6千米,那么他应支付的费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文艺团体为“希望工程”募捐组织了一场义演,共售出1000张票,筹出票款6920元,且每张成人票8元,学生票5元.
(1)问成人票与学生票各售出多少张?
(2)若票价不变,仍售出1000张票,所得的票款可能是7290元吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应政府提出的由中国制造向中国创造转型的号召,某公司自主设计了一款成本为40元的可控温杯,并投放市场进行试销售,经过调查发现该产品每天的销售量y(件)与销售单价x(元)满足一次函数关系:y=﹣10x+1200.
(1)求利润S(元)与销售单价x(元)之间的关系式;
(2)当销售单价定为多少时,该公司每天获取的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com