Question

5．11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题：小溪边长着两棵棕榈树，恰好隔岸相望．一棵树高是30肘尺（肘尺是古代的长度单位），另外一棵高20肘尺；两棵棕榈树的树干间的距离是50肘尺．每棵树的树顶上都停着一只鸟．忽然，两只鸟同时看见棕榈树间的水面上游出一条鱼，它们立刻以相同的速度飞去抓鱼，并且同时到达目标．问这条鱼出现的地方离比较高的棕榈树的树根有多远？

Answer 1

分析 根据题意画出图形，利用勾股定理建立方程，求出x的值即可．

解答 解：画图解决，通过建模把距离转化为线段的长度．
由题意得：AB=20，DC=30，BC=50，
设EC为x肘尺，BE为（50-x）肘尺，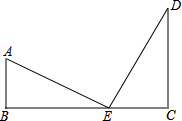
在Rt△ABE和Rt△DEC中，
AE²=AB²+BE²=20²+（50-x）²，DE²=DC²+EC²=30²+x²，
又∵AE=DE，
∴x²+30²=（50-x）²+20²，
x=20，
答：这条鱼出现的地方离比较高的棕榈树的树根20肘尺．

另解：设：这条鱼出现的地方离比较高的棕榈树的树根肘尺，则这条鱼出现的地方离比较低的棕榈树的树根（50-x）肘尺．
得方程：x²+30²=（50-x）²+20²，
可解得：x=20；
答：这条鱼出现的地方离比较高的棕榈树的树根20肘尺．

点评 本题考查勾股定理的正确运用；善于挖掘题目的隐含信息是解决本题的关键．