
【题目】如图,已知![]() 是
是![]() 的外接圆,
的外接圆,![]() ,
,![]() 是劣弧
是劣弧![]() 上的点(不与点
上的点(不与点![]() 、
、![]() 重合),延长
重合),延长![]() 至
至![]() .
.
![]() 求证:
求证:![]() 的延长线
的延长线![]() 平分
平分![]() ;
;
![]() 若
若![]() ,
,![]() 中
中![]() 边上的高为
边上的高为![]() ,求
,求![]() 的面积.
的面积.

【答案】(1)见解析;(2)![]() 的外接圆的面积为
的外接圆的面积为![]() .
.
【解析】
(1)要证明AD的延长线平分∠CDE,即证明∠EDF=∠CDF,转化为证明∠ADB=∠CDF,再根据A,B,C,D四点共圆的性质,和等腰三角形角之间的关系即可得到.
(2)求△ABC外接圆的面积.只需解出圆半径,故作等腰三角形底边上的垂直平分线即过圆心,再连接OC,根据角之间的关系在三角形内即可求得圆半径,可得到外接圆面积.
![]() 证明:如图,设
证明:如图,设![]() 为
为![]() 延长线上一点,
延长线上一点,
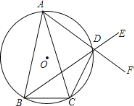
∵![]() ,
,![]() ,
,![]() ,
,![]() 四点共圆,
四点共圆,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
即![]() 的延长线平分
的延长线平分![]() .
.
![]() 设
设![]() 为外接圆圆心,连接
为外接圆圆心,连接![]() 比延长交
比延长交![]() 于
于![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,
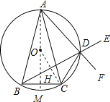
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() ,
,
设圆半径为![]() ,
,
则![]() ,
,
∵![]() 中
中![]() 边上的高为
边上的高为![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() 的外接圆的面积为:
的外接圆的面积为:![]() .
.


科目:初中数学 来源: 题型:
【题目】铜陵市义安区实施了城乡居民基本医疗保险(简称“医疗保险”),办法规定农村村民只要每人每年交纳180元钱就可以加入医疗保险,住院时自己先垫付,出院同时就可得到按一定比例的报销款,这项举措惠及民生,吴斌与同学随机调查了他们镇的一些农民,根据收集到的数据绘制了以下的统计图.
根据图中信息,解答下列问题:
(1)本次调查了多少村民?被调查的村民中参加医疗保险,得到报销款的有多少人?
(2)若该镇有34000村民,请估算有多少人参加了医疗保险?要使两年后参加医疗保险的人数增加到业务31460人,假设这两年的年增长率相同,求年增长率?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 和
和![]() 的平分线相交于点
的平分线相交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,下列四个结论:
,下列四个结论:
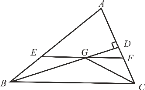
①![]() ; ②
; ②![]() ;
;
③点![]() 到
到![]() 各边的距离相等;
各边的距离相等;
④设![]() ,
,![]() ,则
,则![]() .
.
其中正确的结论有( )
A.①②④B.①②③C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,O是△ABC的内心,以O为圆心,r为半径的圆与线段AB有交点,则r的取值范围是( )
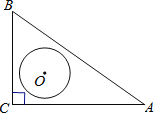
A.r≥1 B.1≤r≤![]() C.1≤r≤
C.1≤r≤![]() D.1≤r≤4
D.1≤r≤4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于O点,过点O作BC的平行线交AB于M点,交AC于N点,则△AMN的周长为( )
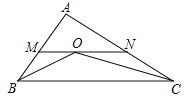
A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的三倍,则称这样的方程为“3倍根方程”,以下说法不正确的是( )
A. 方程x2﹣4x+3=0是3倍根方程
B. 若关于x的方程(x﹣3)(mx+n)=0是3倍根方程,则m+n=0
C. 若m+n=0且m≠0,则关于x的方程(x﹣3)(mx+n)=0是3倍根方程
D. 若3m+n=0且m≠0,则关于x的方程x2+(m﹣n)x﹣mn=0是3倍根方程
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县古田镇某纪念品商店在销售中发现:“成功从这里开始”的纪念品平均每天可售出20件,每件盈利40元.为了扩大销售量,增加盈利,尽快减少库存,该商店在今年国庆黄金周期间,采取了适当的降价措施,改变营销策略后发现:如果每件降价4元,那么平均每天就可多售出8件.商店要想平均每天在销售这种纪念品上盈利1200元,那么每件纪念品应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O半径为1,AB是⊙O的直径,C是⊙O上一点,连接AC,⊙O外的一点D在直线AB上,若AC=![]() ,OB=BD.
,OB=BD.
(1)求证:CD是⊙O的切线;
(2)求阴影部分的面积.(结果保留π)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com