
����Ŀ�����ϱ߷����������������ļ��������У�Ϊ������������˲���ĥ��Ĺ�ѫ.Ϊ���ϱ߷����ӵ�����ִӼס��������ֿ���A��B����Ӫ�����������ʣ���֪�ײֿ�ɵ�����������100�֣��Ҳֿ�ɵ�����������80�֣�A��Ӫ����������70�֣�B��Ӫ����������110�֣����ֿA��B����Ӫ��·�̺��˷����±���
·�̣�ǧ�ף� | �˷ѣ�Ԫ/�֡�ǧ�ף� | |||
�ײֿ� | �Ҳֿ� | �ײֿ� | �Ҳֿ� | |
A��Ӫ | 20 | 15 | 12 | 12 |
B��Ӫ | 25 | 20 | 10 | 8 |
��ײֿ�����A��Ӫ��������Ϊx�֣�xΪ�����������˷�Ϊy��Ԫ��.
��1����y��x�ĺ�������ʽ��Ҳ�ƹ�ϵʽ������ֱ��д��x��ȡֵ��Χ��
��2����Ҫʹ���˷Ѳ�����37160Ԫ���м��������������ʷ������������ͷ������˷����٣�
���𰸡���1��![]() ����2�������������ͷ���. �ײֿ�����A��Ӫ��������70�֣�����B��Ӫ��������30�֣��Ҳֿ�����A��Ӫ��������0�֣�����B��Ӫ��������80��ʱ�����˷�����.
����2�������������ͷ���. �ײֿ�����A��Ӫ��������70�֣�����B��Ӫ��������30�֣��Ҳֿ�����A��Ӫ��������0�֣�����B��Ӫ��������80��ʱ�����˷�����.
��������
��1�����ݡ����˷�=�ײֿ�����A��Ӫ�˷�+�ײֿ�����B��Ӫ�˷�+�Ҳֿ�����A��Ӫ�˷�+�Ҳֿ�����B��Ӫ�˷ѡ��г�������ϵʽ���ɣ�
��2���������˷Ѳ�����37160Ԫ���г�����ʽ����������ͷ������ٽ��һ�κ����������ԣ�������˷����ٵķ�������.
��1���ײֿ�����A��Ӫ��������x�֣�������B��Ӫ��������![]() ��.
��.
�Ҳֿ�����A��Ӫ��������![]() �֣��Ҳֿ�����B��Ӫ��������
�֣��Ҳֿ�����B��Ӫ��������![]() ��.
��.
������ã�
![]()
�֡�![]() �����
�����![]() ��
��
��![]() ����x��ȡֵ��ΧΪ
����x��ȡֵ��ΧΪ![]() .
.
��![]() ��
��
��2��������ã�![]() ��
��
���![]() ��
��
��![]() ����������
����������
��xΪ68��69��70�������������ͷ���.
��һ�κ�����![]() ��
��
��y��ֵ��x���������С��
��![]() ʱ�����˷�y����.
ʱ�����˷�y����.
�𣺼ײֿ�����A��Ӫ��������70�֣�����B��Ӫ��������30�֣��Ҳֿ�����A��Ӫ��������0�֣�����B��Ӫ��������80��ʱ�����˷�����.


 �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
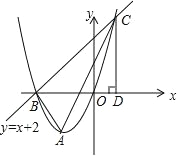
����Ŀ����ͼ����֪������ y��x2+2x �Ķ���Ϊ A��ֱ�� y��x+2 �������߽��� B��C ���㣮
��1���� A��B��C ��������ꣻ
��2���� CD��x ���ڵ� D����֤����ODC�ס�ABC��
��3������ P Ϊ�������ϵ�һ�����㣬���� P �� PM��x ���ڵ� M�����Ƿ��ڳ� C ���������λ�õĵ㣬ʹ�� O��P��M Ϊ��������������ABC ���ƣ� �����ڣ������������ P �����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2011����Ҷ����ƺ�ݳ����Ӵ��˴������ȣ���̨�˲��ƺ�ݳ��Ľ��ij������һͣ�����Կ�����˾����������صĵ��飬���ε����������������������ʱ��ȵ�ƿ��������ѽ�ƻ�Ӳ��Ⱦƣ����ƺ�������רҵ˾�����ݣ���ƽʱ�Ⱦƣ����������첻�Ⱦƣ�����ε���������������Ƴ������в�������ͳ��ͼ������������Ϣ������������⣮
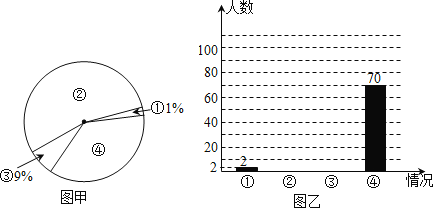
��1���ü��߱���һ������
�� ��˾����
��2����ͼ�������������ε�Բ�Ľǣ�����ȫͼ����
��3���ڱ��ε����У���������ɷ�����һ��˾�����������ڵ���������ĸ��ʣ�
��4��������ڿ�����10����˾���У�Υ�����Ƽ��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��PMN�У���P=90�㣬PM=PN��MN=6cm������ABCD��AB=2cm��BC=10cm����C�͵�M�غϣ���B��C��M����N��ͬһֱ���ϣ���Rt��PMN����������ABCD��MN����ֱ����ÿ��1cm���ٶ������ƶ�������C���N�غ�Ϊֹ�����ƶ�x�����ABCD����PMN�ص����ֵ����Ϊy����y��x�Ĵ���ͼ���ǣ�������
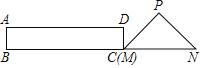
A. 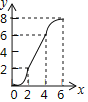 B.
B. 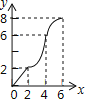 C.
C. 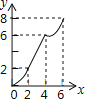 D.
D. 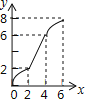
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʮһ�조�����š�������ѧ�����ı�����������������ʦ����ѧ����.��������������99������110��������332��ʦ������.ijУΪ�˽�ȫУѧ���Ա����м����Ŀ��ϲ�������A���й�������B���й������赸��C���й����ա�D��������E���������ݣ�����ȫУѧ���������ȡ����ѧ�������ʾ����飬Ҫ��ÿ��ѧ��ѡ��һ����ϲ���Ľ�Ŀ�����ѵ��������Ƴ�������������ͳ��ͼ.

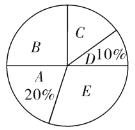
�����������Ϣ������������⣺
��1����α������ѧ�����ж����ˣ�
��2���뽫����ͳ��ͼ��������������ͳ��ͼ�У�B��Ŀ����Ӧ��Բ�Ľ��Ƕ��ٶȣ�
��3������У��2400��ѧ��������ȫУѧ����ϲ���й������赸��Ŀ�Ĺ��ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB��4��BC��6����M��BC���е㣮
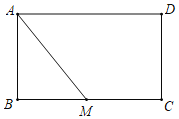
��1����AM������һ��E��ʹ��ADE�ס�MAB���߹���ͼ����д��������
��2���ڣ�1���������£���AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����![]() �У�
�У�![]() ����D��E�ֱ���AB��AC���е㣬��F��BC�ӳ����ϣ�����EF����
����D��E�ֱ���AB��AC���е㣬��F��BC�ӳ����ϣ�����EF����![]() ��
��
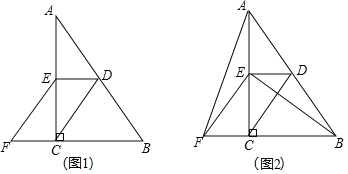
![]() ��ͼ1����֤���ı���CDEF��ƽ���ı��Σ�
��ͼ1����֤���ı���CDEF��ƽ���ı��Σ�
![]() ��ͼ2������AF��BE���ڲ������κθ����ߵ�����£���ֱ��д��ͼ2��������
��ͼ2������AF��BE���ڲ������κθ����ߵ�����£���ֱ��д��ͼ2��������![]() �����ȵ������Σ�
�����ȵ������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
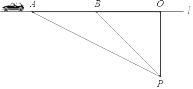
����Ŀ����ͨ��ȫ������ע���ȵ����⣬��ȫ������Ҫ�dz��ٺͳ��أ�ij��ѧ���꼶��ѧ�С���ͬѧ�����˲��������ٶȵ�ʵ�飮��ͼ�����ڱ�ֱ�Ĺ�·1��ѡȡһ��P���ڹ�·1��ȷ����O��B��ʹ��PO��l��PO��100�ף���PBO��45�㣮��ʱ��һ���γ��ڹ�·1����B��A����ʻ������ô˳���B����ʻ��A�����õ�ʱ��Ϊ3�룬����á�APO��60�㣮��·������ÿСʱ80ǧ�ף����жϴ˳��Ƿ��٣���˵�����ɣ��ο����ݣ�![]() ��1.41��
��1.41��![]() ��1.73����
��1.73����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y��a��x��h��2+k��a��0����ͼ��ԭ�㣬���ֵΪ16������״��������y��4x2+2x��3��ͬ����˺����Ĺ�ϵʽΪ_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com