
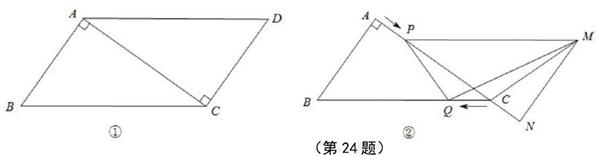
已知:如图①,在□ABCD中,AB=3cm,BC=5cm.AC⊥AB。△ACD沿AC的方向匀速平移得到
△PNM,速度为1cm/s;同时,点Q从点C出发,沿CB方向匀速运动,速度为1cm/s,当△PNM停止平移时,点Q也停止运动.如图②,设运动时间为t(s)(0<t<4).解答下列问题:
(1)当t为何值时,PQ∥MN?
(2)设△QMC的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S△QMC∶S四边形ABQP=1∶4?若存在,求出t的值;
若不存在,请说明理由.
(4)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
解:(1)在Rt△ABC中,由勾股定理得: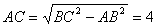
由平移性质可得MN∥AB
因为PQ∥MN,所以PQ∥AB,所以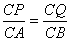 ,即
,即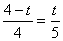 ,解得
,解得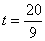
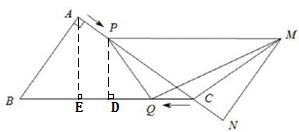 (2)作PD⊥BC于点D,AE⊥BC于点E
(2)作PD⊥BC于点D,AE⊥BC于点E
由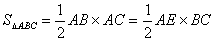 可得
可得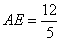
则由勾股定理易求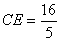
因为PD⊥BC,AE⊥BC
所以AE∥PD,所以△CPD∽△CAE
所以 ,即
,即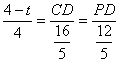
求得: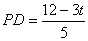 ,
,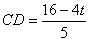
因为PM∥BC,所以M到BC的距离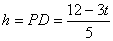
所以,△QCM是面积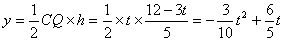
(3)因为PM∥BC,所以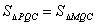
若S△QMC∶S四边形ABQP=1∶4,则S△QMC∶S△ABC=1∶5
即: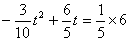 ,整理得:
,整理得: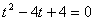 ,解得
,解得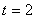
答:当t=2时,S△QMC∶S四边形ABQP=1∶4
(4)若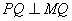 ,则∠MDQ=∠PDQ=90°
,则∠MDQ=∠PDQ=90°
因为MP∥BC,所以∠MPQ=∠PQD,
所以△MQP∽△PDQ,所以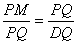 ,所以
,所以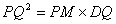
即: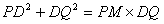 ,由
,由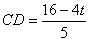 ,所以DQ = CD-CQ
,所以DQ = CD-CQ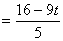
故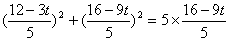 ,整理得
,整理得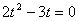
解得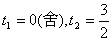
答:当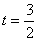 时,
时,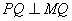 。
。


科目:初中数学 来源: 题型:
某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵.两次共花费940元(两次购进的A、B两种花草价格均分别相同).
(1)A、B两种花草每棵的价格分别是多少元?
(2)若购买A、B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
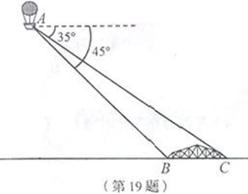
小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为45°
和35°,已知大桥BC与地面在同一水平面上,其长度为100m。请求出热气球离地面的高度。
(结果保留整数,参考数据: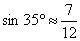 ,
, 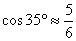 ,
,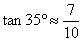
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形. 若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形标号为【 】
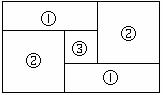
A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
下列各组长度的线段是否成比例?
(1)4 cm,6 cm,8 cm,10 cm;
(2)4 cm,6 cm,8 cm,12 cm;
(3) 11 cm,22 cm,33 cm,66 cm;
(4)4 cm,6 cm,6 cm,9 cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com