
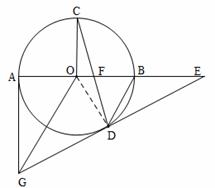
如图所示,AB是⊙O的直径,OC⊥AB,弦CD与OB交于点F,过圆心O作OG∥BD,交过点A所作⊙O的切线于点G,连结GD并延长与AB的延长线交于点E.
(1)求证:GD是⊙O的切线;
(2)试判断△DEF的形状,并说明理由;
(3)若OF:OB=1:3,⊙O的半径为3,求AG的长.

(1)证明:连结OD,如图,
∵AG是过点A的切线,AB是⊙O的直径,
∴AG⊥AB, ∴∠GAB=90°.
∵OG∥BD,
 ∴∠AOG=∠OBD,∠DOG=∠ODB.
∴∠AOG=∠OBD,∠DOG=∠ODB.
∵OC=OB, ∴∠OBD=∠ODB.
∴∠AOG=∠DOG.
在△AOG和△DOG中,
∴△AOG≌△DOG,
∴∠ODG=∠GAB=90°, 即OD⊥DE
∵OD是⊙O的半径,
∴GD是⊙O的切线;
(2)解:△DEF是等腰三角形.理由如下:
由(1)知,OD⊥DE,
∴∠ODE=90°,即∠ODC+∠EDF=90°,
∵OC=OD, ∴∠C=∠ODC,
∴∠EDF+∠C=90°,
而OC⊥OB, ∴∠C+∠OFC=90°, ∴∠OFC=∠EDF,
∵∠DFE=∠OFC, ∴∠EDF=∠DFE,
∴DE=EF, ∴△DEF是等腰三角形. ……7分
(3)解:∵OF:OB=1:3,⊙O的半径为3, ∴OF=1,
在Rt△ODE中,OD=3,DE=x,则EF=x,OE=1+x,
∵OD2+DE2=OE2, ∴32+x2=(x+1)2,解得x=4,
∵DE=EF, ∴DE=4,OE=5,
∵AG为⊙O的切线, ∴AG⊥AE,
∴∠GAE=90°, 而∠OED=∠GEA,
∴Rt△EOD∽Rt△EGA, ∴ =
=  ,即
,即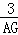 =
= 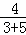 ,
,
∴AG=6. ……11分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
已知关于x的方程x2-2(k-1)x+k2=0有两个实数根x1,x2.
(1)求k的取值范围;(3分)
(2)若x12+ x22=14,求k的值. (4分)
查看答案和解析>>
科目:初中数学 来源: 题型:
在上信息技术课时,张老师布置了一个练习计算机打字速度的学习任务,过了一段时间,张老师发现小聪打一篇1000字 的文章与小明打一篇900字的文章所用的时间相同.已知小聪每分钟比小明每分钟多打5个字,请你求出小聪、小明两人每分钟各打多少个字?
的文章与小明打一篇900字的文章所用的时间相同.已知小聪每分钟比小明每分钟多打5个字,请你求出小聪、小明两人每分钟各打多少个字?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com