
如图①所示,已知A、B为直线a上两点,点C为直线a上方一动点,连接AC、BC,分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG,过点D作DD1┴a于点D1 ,过点E作EE1┴a于点E1。
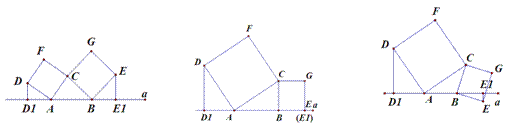 |
图① 图② 图③
⑴如图②,当点E恰好在直线a上时,(此时E1和E重合)。试说明DD1=AB;
⑵如图①中,当D、E两点都在直线a的上方时,试探求三条线段DD1、EE1、AB之间的数量关系,并说明理由。
⑶如图③,当点E在直线a的 下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系。(不需要证明)
下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系。(不需要证明)
(1)证明:∵四边形CADF、CBEG是正方形,
∴AD=CA,∠DAC=∠ABC=90°, (1分)
∴∠DAD1+∠CAB=90°,
∵DD1⊥AB,
∴∠DD1A=∠ABC=90°, 
∴∠DAD1+∠ADD1=90°,
∴∠ADD1=∠CAB,
在△ADD1和△CAB中,
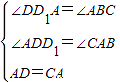 ,
,
∴△ADD1≌△CAB(AAS), (3分)
∴DD1=AB; (4分)
(2)AB=DD1+EE1. (5分)
证明:过点C作CH⊥AB于H,
∵DD1⊥AB,
∴∠DD1A=∠CHA=90°,
∴∠DAD1+∠ADD1=90°,
∵四边形CADF是正方形,
∴AD=CA,∠DAC=90°,
∴∠DAD1+∠CAH=90°,
∴∠ADD1=∠CAH,
在△ADD1和△CAH中,
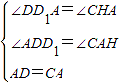 ,
,
∴△ADD1≌△CAH(AAS), (7分)
∴DD1=AH;
同理:EE1=BH, (8分)
∴AB=AH+BH=DD1+EE1; (9分)
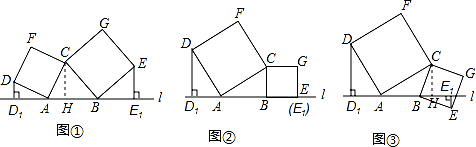
(3)AB=DD1-EE1.(10分)


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
如图,在菱形ABCD中,AB=10,sinA=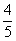 ,点E在AB上,AE=4,过点E作EF∥AD,交CD于点F.
,点E在AB上,AE=4,过点E作EF∥AD,交CD于点F.
(1)请写出菱形ABCD的面积: ;
(2)若点P从点A出发以1个单位长度/秒的速度沿着线段AB向终点B运动,同时点Q从点E出发也以1个单位长度/秒的速度沿着线段EF向终点F运动,设运动时间为t(秒).
①当t=5时,求PQ的长;
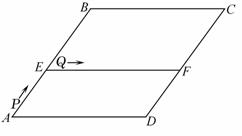 ②以P为圆心,PQ长为半径的⊙P是否能与直线AD相切?如果能,求此时t的值;如果不能,说明理由.
②以P为圆心,PQ长为半径的⊙P是否能与直线AD相切?如果能,求此时t的值;如果不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图四边形ABCD中,已知∠A=∠C=30°,∠D=60°,AD=8,CD=10.
(1)求AB、BC的长;
(2)已知,半径为1的⊙P在四边形ABCD的外面沿各边滚动(无滑动)一周 ,求⊙P在整个滚动过程中所覆盖部分图形的面积.
,求⊙P在整个滚动过程中所覆盖部分图形的面积.
 | |||
 | |||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com