
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
分析 首先把点(-$\frac{1}{2}$,2)代入y=$\frac{k}{x}$中可得k的值,然后再确定y=kx-2的图象不经过第几象限.
解答 解:∵函数y=$\frac{k}{x}$的图象经过点(-$\frac{1}{2}$,2),
∴2=$\frac{k}{-\frac{1}{2}}$,
解得:k=-1,
∴函数y=kx-2=-x-2,
∴图象经过第二三四象限,不经过第一象限.
故选:A.
点评 此题主要考查了一次函数图象与系数的关系,关键是掌握y=kx+b中,
①k>0,b>0?y=kx+b的图象在一、二、三象限;
②k>0,b<0?y=kx+b的图象在一、三、四象限;
③k<0,b>0?y=kx+b的图象在一、二、四象限;
④k<0,b<0?y=kx+b的图象在二、三、四象限.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一种长方形餐桌的四周可以坐6人用餐(带阴影的小长方形表示1个人的位置).现把n张这样的餐桌按如图方式拼接起来.
一种长方形餐桌的四周可以坐6人用餐(带阴影的小长方形表示1个人的位置).现把n张这样的餐桌按如图方式拼接起来.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
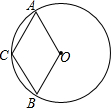 如图,四边形ABCO中,点A,B,C在劣弧$\widehat{AB}$上,则下列结论正确的有①②④(在横线上填写所有正确结论的序号).
如图,四边形ABCO中,点A,B,C在劣弧$\widehat{AB}$上,则下列结论正确的有①②④(在横线上填写所有正确结论的序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
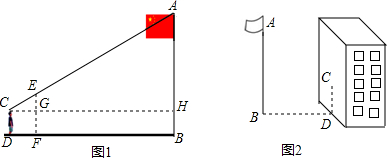
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
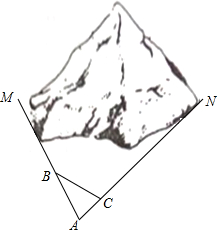 如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.
如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 提出问题:当x>0时如何求函数y=x+$\frac{1}{x}$的最大值或最小值?
提出问题:当x>0时如何求函数y=x+$\frac{1}{x}$的最大值或最小值?| x | … | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | … |
| y | … | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com