
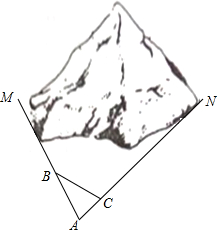
 如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.
如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离. 分析 先根据相似三角形的判定得出△ABC∽△ANM,再利用相似三角形的性质解答即可.
解答 解:在△ABC与△AMN中,
$\frac{AC}{AB}=\frac{30}{54}$=$\frac{5}{9}$,$\frac{AM}{AN}=\frac{1000}{1800}$=$\frac{5}{9}$,∴$\frac{AC}{AB}=\frac{AM}{AN}$,又∵∠A=∠A,
∴△ABC∽△ANM,
∴$\frac{BC}{MN}=\frac{AC}{AM}$,即$\frac{45}{MN}=\frac{30}{1000}$,
解得:MN=1500米,
答:M、N两点之间的直线距离是1500米;
点评 此题考查了相似三角形的判定与性质;熟记相似三角形的判定方法是解决问题的关键.


 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | $\frac{192}{25}$ | D. | $\frac{112}{25}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com