
分析 (1)把A、B两点坐标代入y=kx+b中得到关于k、b的方程组,然后解方程组求出k、b即可得到一次函数解析式;
(2)根据一次函数图象上点的坐标特征,把(a,6)代入一次函数解析式中可求出a的值;
(3)先利用勾股计算出AB的长,然后利用面积法求原点到直线AB的距离.
解答 解:(1)把A(0,3),B(-4,0)代入y=kx+b得$\left\{\begin{array}{l}{b=3}\\{-4k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=3}\end{array}\right.$.
所以一次函数解析式为y=$\frac{3}{4}$x+3;
(2)把(a,6)代入y=$\frac{3}{4}$x+3得$\frac{3}{4}$a+3=6,解得a=4;
(3)AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
设原点到直线AB的距离为h,
则$\frac{1}{2}$•h•5=$\frac{1}{2}$•3•4,
解得h=$\frac{12}{5}$,
所以原点到直线AB的距离为$\frac{12}{5}$.
点评 本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;再将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;然后解方程或方程组,求出待定系数的值,进而写出函数解析式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
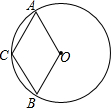 如图,四边形ABCO中,点A,B,C在劣弧$\widehat{AB}$上,则下列结论正确的有①②④(在横线上填写所有正确结论的序号).
如图,四边形ABCO中,点A,B,C在劣弧$\widehat{AB}$上,则下列结论正确的有①②④(在横线上填写所有正确结论的序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
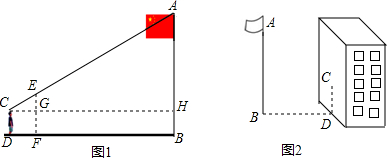
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 营业员 | 小张 | 小王 |
| 月销售件数 | 200 | 150 |
| 月总收入/元 | 1400 | 1250 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
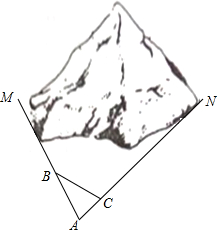 如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.
如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.
如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知点A、B、C的坐标分别A(1,6)、B(1,0)、C(5,0).若点P在∠ABC的平分线上,且PA=PC,则点P的坐标为(6,5).
如图,已知点A、B、C的坐标分别A(1,6)、B(1,0)、C(5,0).若点P在∠ABC的平分线上,且PA=PC,则点P的坐标为(6,5).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com