
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:填空题
 数学活动课上,同学们围绕作图问题:“如图,已知直线l和l外一点P,用直尺和圆规作直线PQ,使PQ⊥l于点Q.”其中一位同学作出了如图所示的图形.你认为他的作法的理由有到线段两端点距离相等的点在这条线段的垂直平分线上;两点确定一条直线.
数学活动课上,同学们围绕作图问题:“如图,已知直线l和l外一点P,用直尺和圆规作直线PQ,使PQ⊥l于点Q.”其中一位同学作出了如图所示的图形.你认为他的作法的理由有到线段两端点距离相等的点在这条线段的垂直平分线上;两点确定一条直线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一种长方形餐桌的四周可以坐6人用餐(带阴影的小长方形表示1个人的位置).现把n张这样的餐桌按如图方式拼接起来.
一种长方形餐桌的四周可以坐6人用餐(带阴影的小长方形表示1个人的位置).现把n张这样的餐桌按如图方式拼接起来.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
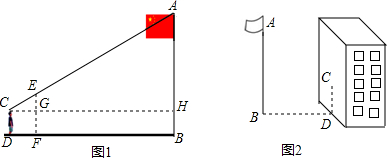
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
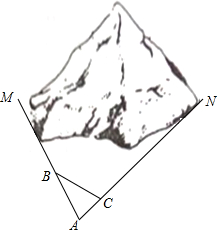 如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.
如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
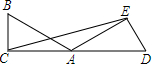 如图,已知∠BAC=40°,把△ABC绕着点A顺时针旋转,使得点B与CA的延长线上的点D重合.
如图,已知∠BAC=40°,把△ABC绕着点A顺时针旋转,使得点B与CA的延长线上的点D重合.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com