
分析 (1)利用同底数幂的除法法则,把括号内的两项分别除以8x2y2即可;
(2)先利用乘法公式展开,然后合并同类项即可;
(3)先化为同分母,再进行同分母的减法运算,然后把分子分解因式后约分即可;
(4)先把括号内通分,再把除法运算化为乘法运算,然后约分即可.
解答 解:(1)原式=$\frac{7}{8}$y-xz;
(2)原式=3(y2-2yz+z2)-(4y2-z2)
=3y2-6yz+3z2-4y2+z2
=-y2-6yz+4z2;
(3)原式=$\frac{{x}^{2}}{x-1}$-$\frac{x}{x-1}$
=$\frac{{x}^{2}-x}{x-1}$
=$\frac{x(x-1)}{x-1}$
=x;
(4)原式=$\frac{a+1}{(a-1)^{2}}$÷$\frac{a-1+2}{a-1}$
=$\frac{a+1}{(a-1)^{2}}$•$\frac{a-1}{a+1}$
=$\frac{1}{a-1}$.
点评 本题考查了整式的混合运算:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.“整体”思想在整式运算中较为常见,适时采用整体思想可使问题简单化,并且迅速地解决相关问题,此时应注意被看做整体的代数式通常要用括号括起来.也考查了分式的混合运算.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
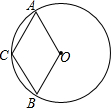 如图,四边形ABCO中,点A,B,C在劣弧$\widehat{AB}$上,则下列结论正确的有①②④(在横线上填写所有正确结论的序号).
如图,四边形ABCO中,点A,B,C在劣弧$\widehat{AB}$上,则下列结论正确的有①②④(在横线上填写所有正确结论的序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 营业员 | 小张 | 小王 |
| 月销售件数 | 200 | 150 |
| 月总收入/元 | 1400 | 1250 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
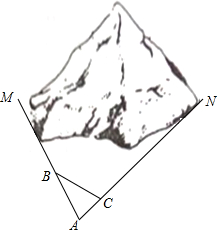 如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.
如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,是一个正方体纸盒展开图,按虚线折成正方体后,若使相对面上的两数互为相反数,则A、B、C表示的数依次是-5,-π,$\frac{3}{2}$.
如图,是一个正方体纸盒展开图,按虚线折成正方体后,若使相对面上的两数互为相反数,则A、B、C表示的数依次是-5,-π,$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.
如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售时间x(周) | 1 | 2 | 3 | 4 | 5 | 6 | … |
| 每千克售价y(元) | 30 | 28 | 26 | 24 | 22 | 20 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com