【题目】已知二次函数
的图象与
轴交于点
、
，且
，与
轴的正半轴的交点在
的下方．下列结论：①
；②
；③
；④
；⑤
．其中正确结论的个数是________个．
【答案】3
【解析】
本题依据二次函数图象的画法画出大致图象，进一步利用方程根与系数的关系等知识和数形结合能力仔细分析即可解．
如图：
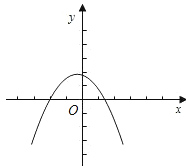
①由图象开口向下知a＜0，由y=ax2+bx+c与x轴的另一个交点坐标为（x1，0 ），且1＜x1＜2，则该抛物线的对称轴为x=﹣
=
＞﹣
，即
＜1，由a＜0，两边都乘以a得：b＞a．
∵a＜0，对称轴x=﹣＜0，∴b＜0；此项错误；
②因为1＜x1＜2，当x=1时，对应图象上的点在x轴上方，所以a+b+c＞0；所以此项错误；
③由y=ax2+bx+c与x轴的交点坐标为（﹣2，0）得：
a×（﹣2）2+b×（﹣2 ）+c=0，即4a﹣2b+c=0，所以③正确；
④由4a﹣2b+c=0得2a﹣b=﹣
，而0＜c＜2，∴－1＜2a﹣b＜0，所以结论正确．
⑤由一元二次方程根与系数的关系知x1x2=
＜﹣2，结合a＜0得2a+c＞0，所以结论正确．
故答案为：正确结论的个数是3个．
故答案为：3．
科目：初中数学 来源： 题型：
【题目】阅读与思考
x2+（p+q）x+pq型式子的因式分解
x2+（p+q）x+pq型式子是数学学习中常见的一类多项式，如何将这种类型的式子分解因式呢？
我们通过学习，利用多项式的乘法法则可知：（x+p）（x+q）＝x2+（p+q）x+pq，因式分解是整式乘法相反方向的变形，利用这种关系可得x2+（p+q）x+pq＝（x+p）（x+q）．
利用这个结果可以将某些二次项系数是1的二次三项式分解因式，例如，将x2﹣x﹣6分解因式．这个式子的二次项系数是1，常数项﹣6＝2×（﹣3），一次项系数﹣1＝2+（﹣3），因此这是一个x2+（p+q）x+pq型的式子．所以x2﹣x﹣6＝（x+2）（x﹣3）．
上述过程可用十字相乘的形式形象地表示：先分解二次项系数，分别写在十字交叉线的左上角和左下角；再分解常数项，分别写在十字交叉线的右上角和右下角；然后交叉相乘，求代数和，使其等于一次项系数，如图所示．
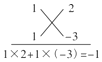
这样我们也可以得到x2﹣x﹣6＝（x+2）（x﹣3）．这种分解二次三项式的方法叫“十字相乘法”．
请同学们认真观察，分析理解后，解答下列问题：
（1）分解因式：y2﹣2y﹣24．
（2）若x2+mx﹣12（m为常数）可分解为两个一次因式的积，请直接写出整数m的所有可能值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（模型建立）（1）如图1，等腰直角三角形ABC中，∠ACB＝90°，CB＝CA，直线ED经过点C，过A作AD⊥ED于点D，过B作BE⊥ED于点E，求证：△BEC≌△CDA．
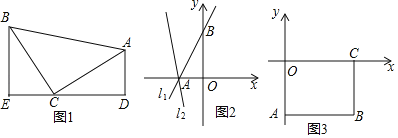
（模型应用）（2）①已知直线l1：y＝
x+3与坐标轴交于点A、B，将直线l1绕点A逆时针旋转45o至直线l2，如图2，求直线l2的函数表达式；
②如图3，长方形ABCO，O为坐标原点，点B的坐标为（8，﹣6），点A、C分别在坐标轴上，点P是线段BC上的动点，若△APD是以点D为直角顶点的等腰直角三角形，当点D在直线y＝﹣2x+5上时，直接写出点D的坐标，并写出整个运动过程中点D的纵坐标n的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】李红在学校的研究性学习小组中负责了解初一年级200名女生掷实心球的测试成绩．她从中随机调查了若干名女生的测试成绩（单位：米），并将统计结果绘制成了如下的统计图表（内容不完整）．
测试成绩 |
|
|
|
|
| 合计 |
频数 | 3 | 27 | 9 | m | 1 | n |
请你结合图表中所提供的信息，回答下列问题：
（1）表中m= ，n= ；
（2）请补全频数分布直方图；
（3）在扇形统计图中，
这一组所占圆心角的度数为 度；
（4）如果掷实心球的成绩达到6米或6米以上为优秀，请你估计该校初一年级女生掷实心球的成绩达到优秀的总人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场销售一批名牌衬衫，平均每天可售出
件，每件盈利
元，为扩大销售增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价一元，市场每天可多售
件，问他降价多少元时，才能使每天所赚的利润最大？并求出最大利润．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
