
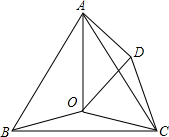
 如图,点O是等边△ABC内一点,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OA和OD.
如图,点O是等边△ABC内一点,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OA和OD.分析 (1)根据旋转的性质可得出OC=OD,结合题意即可证得结论;
(2)找到变化中的不变量,然后利用旋转及全等的性质即可做出解答.
解答 解:(1)∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴CO=CD,∠OCD=60°,
∴△COD是等边三角形.
当α=150°时,△AOD是直角三角形.
理由是:∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴△BOC≌△ADC,
∴∠ADC=∠BOC=150°,
又∵△COD是等边三角形,
∴∠ODC=60°,
∴∠ADO=∠ADC-∠ODC=90°,
∵∠α=150°∠AOB=110°,∠COD=60°,
∴∠AOD=360°-∠α-∠AOB-∠COD=360°-150°-110°-60°=40°,
∴△AOD不是等腰直角三角形,即△AOD是直角三角形.
(2)设∠BOC=α,
①要使AO=AD,需∠AOD=∠ADO,
∵∠AOD=360°-110°-60°-α=190°-α,∠ADO=α-60°,
∴190°-α=α-60°,
∴α=125°;
②要使OA=OD,需∠OAD=∠ADO.
∵∠OAD=180°-(∠AOD+∠ADO)=180°-(190°-α+α-60°)=50°,
∴α-60°=50°,
∴α=110°;
③要使OD=AD,需∠OAD=∠AOD.
∵∠AOD=360°-110°-60°-α=190°-α,
∠OAD=$\frac{18{0}^{°}-(α-6{0}^{°})}{2}$=120°-$\frac{α}{2}$,
∴190°-α=120°-$\frac{α}{2}$,
解得α=140°.
综上所述:当α的度数为125°或110°或140°时,△AOD是等腰三角形.
故答案为:125或110或140.
点评 本题以“空间与图形”中的核心知识(如等边三角形的性质、全等三角形的性质与证明、直角三角形的判定、多边形内角和等)为载体,内容由浅入深,层层递进.试题中几何演绎推理的难度适宜,蕴含着丰富的思想方法(如运动变化、数形结合、分类讨论、方程思想等),能较好地考查学生的推理、探究及解决问题的能力.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,菱形ABCD和菱形ECGF的边长分别为4和6,∠A=120°,则图中阴影部分的面积是( )
如图,菱形ABCD和菱形ECGF的边长分别为4和6,∠A=120°,则图中阴影部分的面积是( )| A. | 8 | B. | 6 | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
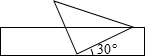 如图,将一个有45°角的三角板的直角顶点放在一张宽为4cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为( )
如图,将一个有45°角的三角板的直角顶点放在一张宽为4cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为( )| A. | 12cm | B. | 8cm | C. | 6$\sqrt{2}$cm | D. | 8$\sqrt{2}$cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com