
【题目】如图,点C,D在线段AB上,CD2=ACDB,且△PCD是等边三角形.
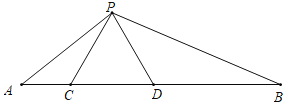
(1)证明:△ACP∽△PDB;
(2)求∠APB的度数.
【答案】(1)见解析;(2)∠APB=120°.
【解析】
(1)通过△PCD是等边三角形,得出∠ACP=∠PDB,再通过CD2=ACDB得出![]() ,从而证明△ACP∽△PDB;
,从而证明△ACP∽△PDB;
(2)由△ACP∽△PDB可得∠APC=∠PBD,进而得出∠APC+∠BPD=60,从而∠APB的度数可求.
(1)∵△PCD是等边三角形,
∴∠PCD=∠PDC=60°,
∴∠ACP=∠PDB=120°,
∵CD2=ACDB,由PC=PD=CD可得:PCPD=ACDB,
即![]() ,
,
∴△ACP∽△PDB;
(2)∵△ACP∽△PDB,
∴∠APC=∠PBD.
∵∠PDB=120°,
∴∠DPB+∠DBP=60°,
∴∠APC+∠BPD=60°.
∴∠APB=∠CPD+∠APC+∠BPD=120°.


科目:初中数学 来源: 题型:
【题目】2019年5月,以“寻根国学,传承文明”为主题的兰州市第三届“国学少年强一国学知识挑战赛”总决赛拉开帷幕,小明晋级了总决赛.比赛过程分两个环节,参赛选手须在每个环节中各选择一道题目.
第一环节:写字注音、成语故事、国学常识、成语接龙(分别用![]() 表示);
表示);
第二环节:成语听写、诗词对句、经典通读(分别用![]() 表示)
表示)
(1)请用树状图或列表的方法表示小明参加总决赛抽取题目的所有可能结果
(2)求小明参加总决赛抽取题目都是成语题目(成语故事、成语接龙、成语听写)的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列条件中不能判定这两个三角形相似的是( )
A. ∠A=55°,∠D=35°
B. AC=9,BC=12,DF=6,EF=8
C. AC=3,BC=4,DF=6,DE=8
D. AB=10,AC=8,DE=15,EF=9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西是我国酿酒最早的地区之一,山西酿酒业迄今为止已有![]() 余年的历史.在漫长的历史进程中,山西人民酿造出品种繁多、驰名中外的美酒佳酿,其中以汾酒、竹叶青酒最为有名.某烟酒超市卖有竹叶青酒,每瓶成本价是
余年的历史.在漫长的历史进程中,山西人民酿造出品种繁多、驰名中外的美酒佳酿,其中以汾酒、竹叶青酒最为有名.某烟酒超市卖有竹叶青酒,每瓶成本价是![]() 元,经调查发现,当售价为
元,经调查发现,当售价为![]() 元时,每天可以售出
元时,每天可以售出![]() 瓶,售价每降低
瓶,售价每降低![]() 元,可多售出
元,可多售出![]() 瓶(售价不高于
瓶(售价不高于![]() 元)
元)
(1)售价为多少时可以使每天的利润最大?最大利润是多少?
(2)要使每天的利润不低于![]() 元,每瓶竹叶青酒的售价应该控制在什么范围内?
元,每瓶竹叶青酒的售价应该控制在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由于各人的习惯不同,双手交叉时左手大拇指或右手大拇指在上是一个随机事件,曾老师对他任教的学生做了一个调查,统计结果如下表所示:
2011届 | 2012届 | 2013届 | 2014届 | 2015届 | |
参与实验的人数 | 106 | 110 | 98 | 104 | 112 |
右手大拇指在上的人数 | 54 | 57 | 49 | 51 | 56 |
频率 | 0.509 | 0.518 | 0.500 | 0.490 | 0.500 |
根据表格中的数据,你认为在这个随机事件中,右手大拇指在上的概率可以估计为( )

A. 0.6 B. 0.5 C. 0.45 D. 0.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个球,分别是红球和白球,这些球除颜色外都相同,将球搅匀,先从中任意摸出一个球,恰好摸到红球的概率为![]() .
.
(1)求口袋中有几个红球?
(2)先从中任意摸出一个球,从余下的球中再摸出一个球,请用列表法或树状图法求两次摸到的球中一个是红球和一个是白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
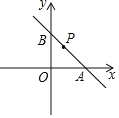
【题目】如图,在平面直角坐标系中,已知,A(2![]() ,0),B(0,2),C(
,0),B(0,2),C(![]() ,0),点P(m,n)为直线AB上一动点,若∠OPC=30°,则m的值为_____.
,0),点P(m,n)为直线AB上一动点,若∠OPC=30°,则m的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤.通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.为保证每天至少售出260斤,张阿姨决定降价销售.
销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com