
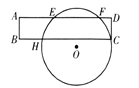
【题目】如图,![]() 经过矩形
经过矩形![]() 的顶点
的顶点![]() ,且与
,且与![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 在圆心
在圆心![]() 同侧.已知
同侧.已知![]() ,
,![]() .
.
(1)![]() 的长为__________.
的长为__________.
(2)若![]() 的半径长为
的半径长为![]() ,则
,则![]() ________.
________.
【答案】6 ![]()
【解析】
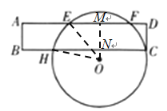
(1)过点O作OM⊥EF,垂足为M,且交BC于点N,由垂径定理得,NH=CN,EM=FM,又由四边形ABNM为矩形,可知BN=AM,可求得HN的长,进而求出CH的长;
(2)连接OE,OH,根据勾股定理分别求出,OM,ON的长,根据AB=MN,可求得AB的 长.
解:(1)过点O作OM⊥EF,垂足为M,且交BC于点N,
∵四边形ABCD为矩形,∴OM⊥BC,
∴四边形ABNM也为矩形.
∴BN=AM.
由垂径定理可得,EM=FM=2,NH=CN.
∴BN=AM=4+2=6,
∴NH=BN-BH=6-3=3.
∴CH=2NH=6.
(2)连接OE,OH,
在Rt△EMN中,由勾股定理可得,OM=![]() ,
,
在Rt△ONH中,由勾股定理可得,ON=![]() ,
,
∴AB=MN=OM-ON=![]() -1.
-1.
故答案为:(1)6;(2)![]() -1.
-1.


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).
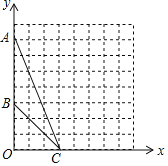
(1)在图中作出△ABC的外接圆⊙P(保留必要的作图痕迹,不写作法)
(2) 若在x轴的正半轴上有一点D(异与C点),且∠ADB=∠ACB,则点D的坐标为 .
(3)若用扇形PAC围成一个圆锥,那么这个圆锥的底面半径为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
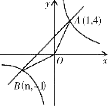
【题目】如图,已知反比例函数![]() 的图象与一次函数y=x+b的图象交于点A(1,4),点B(n,-1).
的图象与一次函数y=x+b的图象交于点A(1,4),点B(n,-1).
(1)求n和b的值;
(2)直接写出一次函数值小于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax+bx+c(a≠0)的图象如图所示,以下结论中正确的个数是( )
①abc>0、②3a>2b、③m(am+b)≤a﹣b(m为任意实数)、④4a﹣2b+c<0.
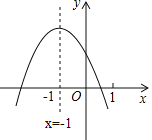
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技馆是少年儿童节假日游玩的乐园.如图所示,图中点的横坐标表示科技馆从8:30开门后经过的时间(分钟),纵坐标表示到达科技馆的总人数.图中曲线对应的函数解析式为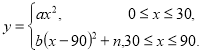 ,10:00之后来的游客较少可忽略不计.
,10:00之后来的游客较少可忽略不计.
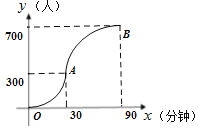
(1)请写出图中曲线对应的函数解析式;
(2)为保证科技馆内游客的游玩质量,馆内人数不超过684人,后来的人在馆外休息区等待.从10:30开始到12:00馆内陆续有人离馆,平均每分钟离馆4人,直到馆内人数减少到624人时,馆外等待的游客可全部进入.请问馆外游客最多等待多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与X轴交于点(―3,0),其对称轴为直线
与X轴交于点(―3,0),其对称轴为直线![]() ,结合图象分析下列结论:①
,结合图象分析下列结论:①![]() ; ②
; ②![]() ;③当
;③当![]() 时,y 随x 的增大而增大,④一元二次方程
时,y 随x 的增大而增大,④一元二次方程![]() 的两根分别为
的两根分别为![]() ;⑤若
;⑤若![]() (
(![]() )为方程
)为方程![]() 的两个根,则
的两个根,则![]() 且
且![]() ,其中正确的结论有( )
,其中正确的结论有( )
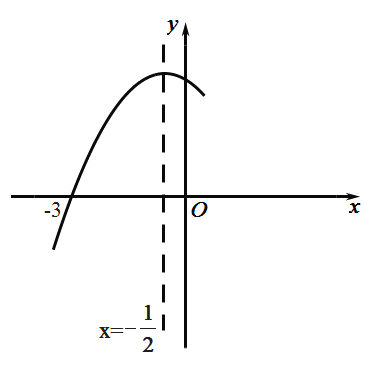
A.3个B.4个C.5个D.6个
查看答案和解析>>
科目:初中数学 来源: 题型:
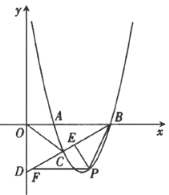
【题目】如图,抛物线![]() 与x轴交于A,B两点,抛物线上另有一点 C在x轴下方,且使ΔOCA∽ΔOBC.
与x轴交于A,B两点,抛物线上另有一点 C在x轴下方,且使ΔOCA∽ΔOBC.
(1)求线段OC的长度;
(2)设直线BC与y轴交于点D,点C是BD的中点时,求直线BD和抛物线的解析式,
(3)在(2)的条件下,点P是直线BC下方抛物线上的一点,过P作![]() 于点E,作PF//AB交BD于点F,是否存在一点P,使得
于点E,作PF//AB交BD于点F,是否存在一点P,使得![]() 最大,若存在,请求出该最大值;若不存在,请说明理由.
最大,若存在,请求出该最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若干名工人某天生产同一种玩具,生产的玩具数整理成条形图(如图所示).则他们生产的玩具数的平均数、中位数、众数分别为( )

A.5,5,4 B.5,5,5
C.5,4,5 D.5,4,4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2x﹣3.
(1)抛物线与x的交点坐标是 ,顶点是 .
(2)选取适当的数据填入下表.在直角坐标系中利用五点法画出此抛物线的图象.
X | … | … | |||||
y | … | … |
(3)结合函数图象,回答下题:
若抛物线上两点A(x1,y1),B(x2,y2)的横坐标满足x1<x2<1比较y1,y2的大小: .当y<0,自变量x的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com