Question

4．已知，如图，△ABC是直角三角形，∠ACB=90°，∠ABC=60°，BC=6cm，点P由C开始向点B以1cm/s的速度运动，点Q由B开始向点A以2cm/s的速度运动，若PQ同时开始运动
（1）运动多少秒时△PQB是直角三角形？
（2）运动多少秒时△PBQ的面积是△ABC面积的$\frac{2}{9}$？
（3）运动多少秒时PQ的长度是$\frac{\sqrt{63}}{2}$cm？

Answer 1

分析 先根据动点的速度、时间表示路程为：PC=t，BQ=2t，BP=6-2t，计算出走完全程的总时间为6秒，
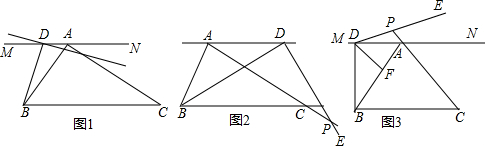
（1）分两种情况：①当∠BQP=90°时，如图1②当∠QPB=90°时，如图2，根据30°所对的直角边等于斜边的一半列式求出时间；
（2）如图3，作△PBQ的高线QD，根据平行线分线段成比例定理求出QD=$\sqrt{3}$t，利用△PBQ的面积是△ABC面积的$\frac{2}{9}$列式可求出t的值；
（3）如图3，在Rt△PQD中，根据勾股定理列方程：$（\frac{\sqrt{63}}{2}）^{2}$=$（\sqrt{3}t）^{2}$+（6-2t）²，求出t的值，都符合题意．

解答 解：设运动时间为t秒，则PC=t，BQ=2t，BP=6-2t，
∵BC=6，
∴点P走完全程需要6秒，
∵∠ACB=90°，∠ABC=60°，BC=6cm，
∴AB=12，
∴点Q走完全程需要6秒，
∴0≤t≤6，
（1）△PQB是直角三角形时，有两种情况：
①当∠BQP=90°时，如图1，
∵∠B=60°，
∴∠BPQ=30°，
∴BP=2BQ，
∴6-2t=2×2t，
t=1，
②当∠QPB=90°时，如图2，
∵∠B=60°，
∴∠BQP=30°，
∴BQ=2BP，
∴2t=2（6-2t），
t=2，
答：运动1秒或2秒时，△PQB是直角三角形；
（2）如图3，过Q作QD⊥BC于D，
在Rt△ACB中，AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$，
∵QD∥AC，
∴$\frac{QD}{AC}=\frac{BQ}{AB}$，
∴$\frac{QD}{6\sqrt{3}}$=$\frac{2t}{12}$，
∴QD=$\sqrt{3}$t，
∵S_△PBQ=$\frac{2}{9}$S_△ABC，
∴$\frac{1}{2}$BP•QD=$\frac{2}{9}$×$\frac{1}{2}$BC×AC，
$\sqrt{3}$t（6-t）=$\frac{2}{9}$×6×$6\sqrt{3}$，
t²-6t+8=0，
解得：t₁=2，t₂=4；
答：运动2秒或4秒时，△PBQ的面积是△ABC面积的$\frac{2}{9}$；
（3）如图3，在Rt△BQD中，∠B=60°，
∴∠BQD=30°，
∴BD=$\frac{1}{2}$BQ=t，
∴PD=PB-BD=6-t-t=6-2t，
由勾股定理得：PQ²=QD²+PD²，
$（\frac{\sqrt{63}}{2}）^{2}$=$（\sqrt{3}t）^{2}$+（6-2t）²，
解得：t₁=$\frac{3}{2}$，t₂=$\frac{27}{14}$，
答：运动$\frac{3}{2}$秒或$\frac{27}{14}$秒时PQ的长度是$\frac{\sqrt{63}}{2}$cm．

点评 本题是一元二次方程的应用，属于动点运动问题，此类题的解题思路为：①确定有几个动点，②动点的行动路线，③时间、速度、会表示路程，④从题中找一等量关系式，列方程即可．