
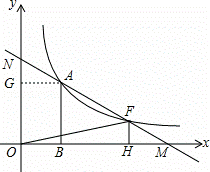
已知反比例函数y=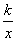 (x>0)的图象经过点A(2,a)(a>0),过点A作AB⊥x轴,垂足为点B,将线段AB沿x轴正方向平移,与反比例函数y=
(x>0)的图象经过点A(2,a)(a>0),过点A作AB⊥x轴,垂足为点B,将线段AB沿x轴正方向平移,与反比例函数y=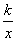 (x>0)的图象相交于点F(p,q).
(x>0)的图象相交于点F(p,q).
(1)当F点恰好为线段的中点时,求直线AF的解析式 (用含a的代数式表示);
(2)若直线AF分别与x轴、y轴交于点M、N,当q=-a2+5a时,令S=S△ANO+S△MFO(其中O是原点),求S的取值范围.
(1)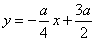 ;(2)10<S<16.
;(2)10<S<16.
【解析】
试题分析:(1)先把点A(2,a)代入反比例函数y=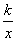 (x>0)求出k的值,再根据F为线段的中点可知F的纵坐标为
(x>0)求出k的值,再根据F为线段的中点可知F的纵坐标为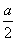 ,把y=
,把y=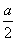 代入y=
代入y=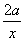 可得出x的值,进而得出点F的坐标,利用待定系数求出直线AF的解析式即可;
可得出x的值,进而得出点F的坐标,利用待定系数求出直线AF的解析式即可;
(2)根据点F(p,q) 在反比例函数y=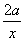 的图象上且q=-a2+5a可得出F点的坐标,故可得出直线AF的解析式,进而得出M、N的坐标,过A作AG⊥y轴于点G,则可得出AG,ON,OM,FH的长,根据S=S△ANO+S△MFO=
的图象上且q=-a2+5a可得出F点的坐标,故可得出直线AF的解析式,进而得出M、N的坐标,过A作AG⊥y轴于点G,则可得出AG,ON,OM,FH的长,根据S=S△ANO+S△MFO=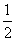 •ON•AG+
•ON•AG+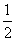 OM•FH可得出关于S、a的二次函数,根据a的取值范围即可得出结论.
OM•FH可得出关于S、a的二次函数,根据a的取值范围即可得出结论.
试题解析:(1)∵反比例函数y=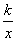 (x>0)的图象经过点A(2,a)(a>0),
(x>0)的图象经过点A(2,a)(a>0),
∴k=2a,
∴y=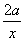 ,
,
∵F为线段的中点,
∴F的纵坐标为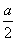 ,把y=
,把y=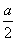 代入y=
代入y=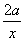 得x=4
得x=4
∴F(4,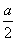 ),
),
设直线AF的解析式为y=k1x+b,
∴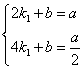 ,
,
解得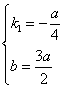 ,
,
∴直线AF的解析式为: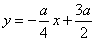 ;
;
(2)∵F(p,q) 在反比例函数y=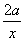 的图象上,
的图象上,
∴q=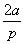 ,
,
∵q=-a2+5a,
∴p=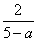 ,
,
∴F(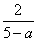 ,-a2+5a)
,-a2+5a)
∴直线AF的解析式为:y=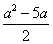 x+(6a-a2),
x+(6a-a2),
∴N(0,6a-a2),M(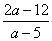 ,0),
,0),
过A作AG⊥y轴于点G,
则AG=2,ON=6a-a2,OM=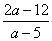 ,FH=-a2+5a
,FH=-a2+5a
S=S△ANO+S△MFO=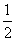 •ON•AG+
•ON•AG+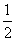 OM•FH
OM•FH
=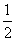 ×2×(6a-a2)+
×2×(6a-a2)+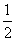 •
•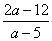 •(-a2+5a)
•(-a2+5a)
=-2a2+12a
=-2(a-3)2+18
∵q>0,q<a,
∴4<a<5.
∴由函数性质可知,10<S<16.
【难度】困难


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
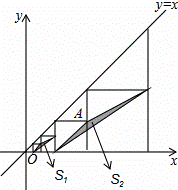
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则Sn的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
已知一次函数y=kx+b的图象经过点(-1,-5),且与正比例函数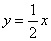 的图象相交于点(2,a).
的图象相交于点(2,a).
(1)求a的值.
(2)求一次函数y=kx+b的表达式.
(3)在同一坐标系中,画出这两个函数的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
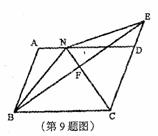
如图,在□ABCD中,∠BCD的平分线CN交□ABCD的边AD 于点N,BF⊥CN, 交CN于点F,交CD的延长线于点E,连接BN、 NE,若 BN=6,BC=8,则 △DNE 的周长为( )•
(A) 14 (B) 11 (C)9 (D) 12
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:AD、BC是⊙O的两条互相垂直的弦,垂足为E,H是弦BC的中点,AO是 ∠DAB的平分线,半径OA交弦CB于点M.
(1)如图1,延长OH交AB于点N,求证:ONB=2ZAON;
(2)如图2,若点M是OA的中点,求证:AD=40H;
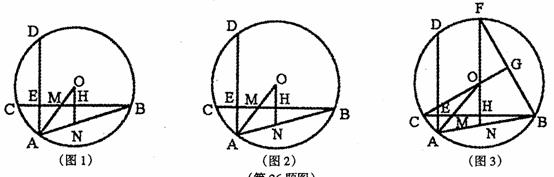 ⑶ 如图3,延长HO交00于点F,连接BF,若C0的延长线交BF于点G,CG丄BF,CH=
⑶ 如图3,延长HO交00于点F,连接BF,若C0的延长线交BF于点G,CG丄BF,CH=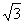 , 求⊙0的半径长.
, 求⊙0的半径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com