
【题目】某校课程中心为了了解学生对开设的3D打印、木工制作、机器人和电脑编程四门课程的喜爱程度,随机调查了部分学生,每人只能选一项最喜爱的课程.图①是四门课程最喜爱人数的扇形统计图,图②是四门课程男、女生最喜爱人数的条形统计图.
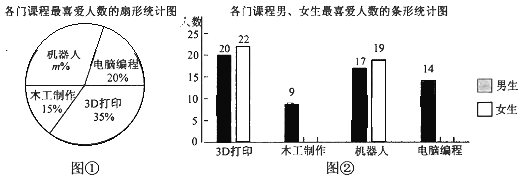
(1)求图①中![]() 的值,补全图②中的条形统计图,标上相应的人数;
的值,补全图②中的条形统计图,标上相应的人数;
(2)若该校共有1800名学生,则该校最喜爱3D打印课程的学生约有多少人?
【答案】(1)m=30,图形见详解
(2)630
【解析】
(1)用100%分别减去电脑编程,3D打印,木工制作的百分比即可求出m,根据喜爱机器人的总人数为36,用36除以30%即可求出总人数,再由总人数分别计算出木工制作和电脑编程的人数即可;(2)用1800×35%即可解题.
解:(1)1-15%-35%-20%=30%,
∴m=30,
∴总人数=36÷30%=120人,
其中木工制作=120×15%=18人,所以女生有18-9=9人,
电脑编程=120×20%=24人, 所以女生有24-14=10人,
补全统计图见下图,
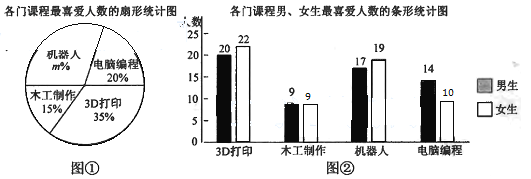
(2)1800×35%=630人,
∴该校最喜爱3D打印课程的学生约有630人.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:
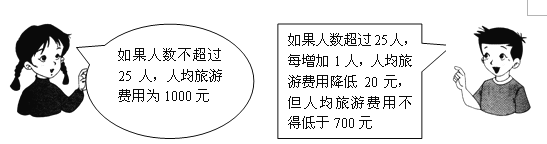 某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
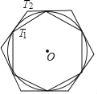
【题目】T1、T2分别为⊙O的内接正六边形和外切正六边形.设T1的半径r,T1、T2的边长分别为a、b,T1、T2的面积分别为S1、S2.下列结论:①r:a=1:1;②r:b=![]() ;③a:b=1:
;③a:b=1:![]() ;④S1:S2=3:4.其中正确的有_____.(填序号)
;④S1:S2=3:4.其中正确的有_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
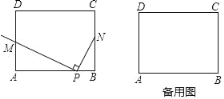
【题目】如图,在矩形ABCD中,AB=4,AD=3,点N为BC边上的一点,且BN=n(n>0),动点P从点A出发,以每秒1个单位长的速度沿AB边向点B运动,连接NP,作射线PM⊥NP交AD于点M,设点P运动的时间是t秒(t>0).
(1)当点M与点A重合时,t等于多少秒,当点M与点D重合时,n等于多少(用含字母t的代数式表示)
(2)若n=2,则
①在点P运动过程中,点M是否可以到达线段AD的延长线上?通过计算说明理由;
②连接ND,当t为何值时,ND∥PM?
(3)过点N作NK∥AB,交AD于点K,若在点P运动过程中,点K与点M不会重合,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
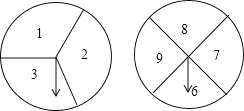
【题目】如图是两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有相应的数字![]() 小强和小宁利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,指针所指区域内的两数字之和小于9,小宁获胜;指针所指区域内的两数字之和等于9为平局;指针所指区域内的两数字之和大于9,小强获胜
小强和小宁利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,指针所指区域内的两数字之和小于9,小宁获胜;指针所指区域内的两数字之和等于9为平局;指针所指区域内的两数字之和大于9,小强获胜![]() 如果指针恰好指在分割线上,那么重转一次.
如果指针恰好指在分割线上,那么重转一次.
![]() 画树状图表示所有可能出现的结果,并指出小宁获胜的概率;
画树状图表示所有可能出现的结果,并指出小宁获胜的概率;
![]() 该游戏规则对小宁,小强是否公平?如公平,请说明理由,如不公平,请修改游戏规则,使游戏公平.
该游戏规则对小宁,小强是否公平?如公平,请说明理由,如不公平,请修改游戏规则,使游戏公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
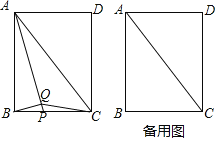
【题目】如图,在矩形ABCD中,AC为对角线,点P为BC边上一动点,连接AP,过点B作BQ⊥AP,垂足为Q,连接CQ.
⑴证明:△ABP∽△BQP;
⑵当点P为BC的中点时,若∠BAC=37°,求∠CQP的度数;
⑶当点P运动到与点C重合时,延长BQ交CD于点F,若AQ=AD,则![]() 等于多少.
等于多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD=![]() ,求
,求![]() 的值.
的值.
(3)(3分)在(2)的条件下,设⊙O的半径为3,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2018双十一购物狂欢节”,阿里巴巴天猫在开场的2分5秒交易额超100亿元.刘老师为此提前花88元购买了一张“88VIP”卡,使用此卡可享受部分特定商品九五折.
(1)为了使买的“88VIP”卡不亏,刘老师应至少选购多少元特定商品?
(2)刘老师在“双十一”到来之前,分别在两家店里选了一套标价为1100元的书籍和一件标价为990元的羽绒服.据了解,双十一当天书籍可以使用“88VIP”卡,并降价![]() ;同时,刘老师发现聪明的老板先将羽绒服提价
;同时,刘老师发现聪明的老板先将羽绒服提价![]() ,双十一当天再降价
,双十一当天再降价![]() .最后刘老师双十一购买两种商品所花费的总金额恰好是 (1) 中的最小值,求m的值.
.最后刘老师双十一购买两种商品所花费的总金额恰好是 (1) 中的最小值,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
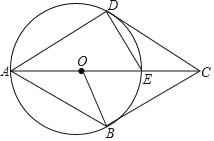
【题目】已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D,点B在⊙O上,连接OB.
(1)求证:DE=OE;
(2)若CD∥AB,求证:BC是⊙O的切线;
(3)在(2)的条件下,求证:四边形ABCD是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com