
【题目】已知a,b,c是△ABC的三边,若a,b,c满足a2-6a+b2-8b+![]() +25=0,则△ABC是_____________三角形;若a,b,c满足a2+b2+c2-ab-bc-ac=0,则△ABC是_________三角形.
+25=0,则△ABC是_____________三角形;若a,b,c满足a2+b2+c2-ab-bc-ac=0,则△ABC是_________三角形.
【答案】直角; 等边.
【解析】
把25分成9、16,利用配方法把a2-6a+b2-8b+![]() +25=0改写为(a-3)2+(b-4)2+
+25=0改写为(a-3)2+(b-4)2+![]() =0,利用非负数的性质求出a、b、c的值,根据勾股定理逆定理判断即可;利用配方法把a2+b2+c2-ab-bc-ac=0改写为(a-b)2+(b-c)2+(a-c)2=0,再利用非负数的性质,可分别求出a、b、c的的关系.
=0,利用非负数的性质求出a、b、c的值,根据勾股定理逆定理判断即可;利用配方法把a2+b2+c2-ab-bc-ac=0改写为(a-b)2+(b-c)2+(a-c)2=0,再利用非负数的性质,可分别求出a、b、c的的关系.
∵a2-6a+b2-8b+![]() +25=0,
+25=0,
∴(a-3)2+(b-4)2+![]() =0,
=0,
∴a=3,b=4,c=5,
∵32+42=52,
∴△ABC是直角三角形;
∵a2+b2+c2-ab-bc-ac=0,
∴(a-b)2+(b-c)2+(a-c)2=0,
∴a=b,b=c,a=c,
∴a=b=c,
∴△ABC是等边三角形.
故答案为:直角;等边.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,CE⊥AB,CF⊥AD.试说明:
(1)△CBE≌△CDF;
(2)AB+DF=AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人从![]() 地前往
地前往![]() 地,甲的速度是每小时80千米,乙的速度是甲的速度的1.5倍,甲比乙早出发0.5小时,结果甲比乙晚到1.5小时.
地,甲的速度是每小时80千米,乙的速度是甲的速度的1.5倍,甲比乙早出发0.5小时,结果甲比乙晚到1.5小时.
(1)求![]() ,
,![]() 两地的路程是多少千米?
两地的路程是多少千米?
(2)当甲到达![]() 地后,乙再与甲同时从
地后,乙再与甲同时从![]() 地按各自的原速返回
地按各自的原速返回![]() 地,若他们由
地,若他们由![]() 地返回
地返回![]() 地的过程中所行走路程的和为180千米,则甲走了多少小时?
地的过程中所行走路程的和为180千米,则甲走了多少小时?
(3)若乙到达![]() 地后立即按原速返回,问再经过多长时间甲与乙之间的距离为20千米?
地后立即按原速返回,问再经过多长时间甲与乙之间的距离为20千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点D是△ABC所在平面内一点,连接AD、CD.
(1)如图1,若∠A=28°,∠B=72°,∠C=11°,求∠ADC;
(2)如图2,若存在一点P,使得PB平分∠ABC,同时PD平分∠ADC,探究∠A,∠P,∠C的关系并证明;
(3)如图3,在 (2)的条件下,将点D移至∠ABC的外部,其它条件不变,探究∠A,∠P,∠C的关系并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),则点B2018的坐标为_____.
,0),B(0,2),则点B2018的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
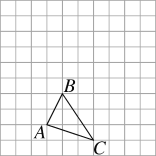
【题目】如图,已知单位长度为1的方格中有三角形ABC.
(1)请画出三角形ABC向上平移3格再向右平移2格所得的三角形A′B′C′;
(2)请以点A为坐标原点建立平面直角坐标系(在图中画出),然后写出点B,B′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
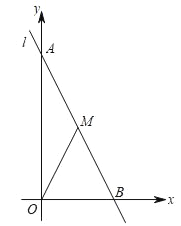
【题目】如图,已知在平面直角坐标中,直线l:y=﹣2x+6分别交两坐标于A、B两点,M是级段AB上一个动点,设点M的横坐标为x,△OMB的面积为S.
(1)写出S与x的函数关系式;
(2)当△OMB的面积是△OAB面积的![]() 时,求点M的坐标;
时,求点M的坐标;
(3)当△OMB是以OB为底的等腰三角形,求它的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,OP为一墙面,它与地面OQ垂直,有一根木棒AB如图放置,点C是它的中点,现在将木棒的A点在OP上由A点向下滑动,点B由O点向OQ方向滑动,直到AB横放在地面为止.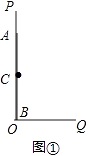
(1)在AB滑动过程中,点C经过的路径可以用下列哪个图象来描述( )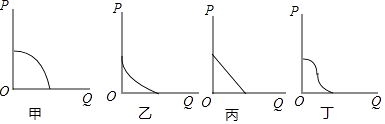
(2)若木棒长度为2m,如图②射线OM与地面夹角∠MOQ=60°,当AB滑动过程中,与OM并于点D,分别求出当AD= ![]() 、AD=1、AD=
、AD=1、AD= ![]() 时,OD的值.
时,OD的值.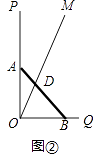
(3)如图③,是一个城市下水道,下水道入口宽40cm,下水道水平段高度为40cm,现在要想把整根木棒AB通入下水道水平段进行工作,那么这根木棒最长可以是(cm)(直接写出结果,结果四舍五入取整数).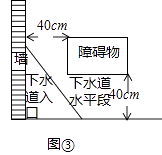
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com