
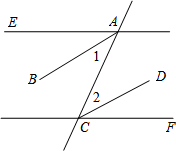
 如图,直线AE、CF分别被直线AC所截,已知AE∥FC,AB平分∠EAC,CD平分∠ACF,将下列说明AB∥CD的过程及理由填写完整.
如图,直线AE、CF分别被直线AC所截,已知AE∥FC,AB平分∠EAC,CD平分∠ACF,将下列说明AB∥CD的过程及理由填写完整.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
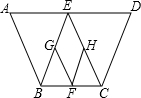 如图,等腰梯形ABCD中,AD∥BC,AB=CD,点E是线段AD上的一个动点(E与A、D不重合),G、F、H分别是BE、BC、CE的中点.
如图,等腰梯形ABCD中,AD∥BC,AB=CD,点E是线段AD上的一个动点(E与A、D不重合),G、F、H分别是BE、BC、CE的中点.查看答案和解析>>
科目:初中数学 来源: 题型:
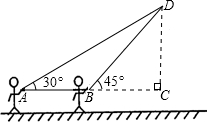 放风筝是大家喜爱的一种运动.星期天的上午小明在大洲广场上放风筝.如图他在A处时不小心让风筝挂在了一棵树的树梢上,风筝固定在了D处.此时风筝线AD与水平线的夹角为30°,AD=8米,为了便于观察.小明迅速向前边移动边收线到达了B处,此时风筝线BD与水平线的夹角为45°.已知点A、B、C在冋一条直线上,∠ACD=90°.请你求出小明此吋所收回的风筝线的长度是多少米?
放风筝是大家喜爱的一种运动.星期天的上午小明在大洲广场上放风筝.如图他在A处时不小心让风筝挂在了一棵树的树梢上,风筝固定在了D处.此时风筝线AD与水平线的夹角为30°,AD=8米,为了便于观察.小明迅速向前边移动边收线到达了B处,此时风筝线BD与水平线的夹角为45°.已知点A、B、C在冋一条直线上,∠ACD=90°.请你求出小明此吋所收回的风筝线的长度是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:
| 摄氏温度x | … | 0 | 10 | 20 | 30 | 40 | 50 | … |
| 华氏温度y | … | 32 | 50 | 68 | 86 | 104 | 122 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、平行四边形的对边相等 |
| B、四条边都相等的四边形是菱形 |
| C、矩形的两条对角线互相垂直 |
| D、对角线互相平分的四边形是平行四边形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com