
【题目】在![]() ABCD中,∠ADC的平分线交直线BC于点E、交AB的延长线于点F,连接AC.
ABCD中,∠ADC的平分线交直线BC于点E、交AB的延长线于点F,连接AC.
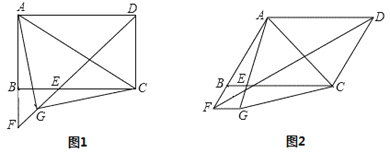
(1)如图1,若∠ADC=90°,G是EF的中点,连接AG、CG.
①求证:BE=BF;
②请判断△AGC的形状,并说明理由.
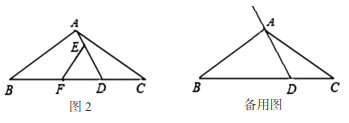
(2)如图2,若∠ADC=60°,将线段FB绕点F顺时针旋转60°至FG,连接AG、CG,判断△AGC的形状.(直接写出结论不必证明)
【答案】(1)①证明见解析;②△AGC是等腰直角三角形.证明见解析;(2)△AGC是等边三角形.
【解析】试题分析:(1)①先判定四边形ABCD是矩形,再根据矩形的性质可得∠ABC=90°,AB∥DC,AD∥BC,然后根据平行线的性质求出∠F=∠FDC,∠BEF=∠ADF,再根据DF是∠ADC的平分线,利用角平分线的定义得到∠ADF=∠FDC,从而得到∠F=∠BEF,然后根据等角对等边的性质即可证明;
②连接BG,根据等腰直角三角形的性质可得∠F=∠BEF=45°,再根据等腰三角形三线合一的性质求出BG=FG,∠F=∠CBG=45°,然后利用“边角边”证明△AFG和△CBG全等,根据全等三角形对应边相等可得AG=CG,再求出∠GAC+∠ACG=90°,然后求出∠AGC=90°,然后根据等腰直角三角形的定义判断即可;
(2)连接BG,根据旋转的性质可得△BFG是等边三角形,再根据角平分线的定义以及平行线的性质求出AF=AD,平行四边形的对角相等求出∠ABC=∠ADC=60°,然后求出∠CBG=60°,从而得到∠AFG=∠CBG,然后利用“边角边”证明△AFG和△CBG全等,根据全等三角形对应边相等可得AG=CG,全等三角形对应角相等可得∠FAG=∠BCG,然后求出∠GAC+∠ACG=120°,再求出∠AGC=60°,然后根据等边三角形的判定方法判定即可.
试题解析:(1)证明:①∵四边形ABCD是平行四边形,∠ADC=90°,
∴四边形ABCD是矩形,∴∠ABC=90°,AB∥DC,AD∥BC,
∴∠F=∠FDC,∠BEF=∠ADF,
∵DF是∠ADC的平分线,∴∠ADF=∠FDC,∴∠F=∠BEF,
∴BF=BE;
②△AGC是等腰直角三角形.
理由如下:连接BG,
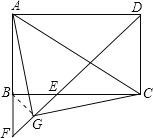
由①知,BF=BE,∠FBC=90°,∴∠F=∠BEF=45°,
∵G是EF的中点,∴BG=FG,∠F=∠CBG=45°,
∵∠FAD=90°,∴AF=AD,又∵AD=BC,∴AF=BC,
在△AFG和△CBG中, 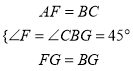 ∴△AFG≌△CBG,
∴△AFG≌△CBG,
∴AG=CG,∠FAG=∠BCG,
又∵∠FAG+∠GAC+∠ACB=90°,∴∠BCG+∠GAC+∠ACB=90°,
即∠GAC+∠ACG=90°,∴∠AGC=90°,∴△AGC是等腰直角三角形;
(2)△AGC是等边三角形.
证明:连接BG,∵FB绕点F顺时针旋转60°至FG,
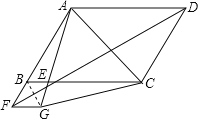
∴△BFG是等边三角形,
∴FG=BG,∠FBG=60°,
又∵四边形ABCD是平行四边形,∠ADC=60°,
∴∠ABC=∠ADC=60°
∴∠CBG=180°-∠FBG-∠ABC=180°-60°-60°=60°,
∴∠AFG=∠CBG,
∵DF是∠ADC的平分线,
∴∠ADF=∠FDC,
∵AB∥DC,
∴∠AFD=∠FDC,
∴∠AFD=∠ADF,
∴AF=AD,
在△AFG和△CBG中,
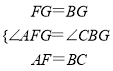 ,
,
∴△AFG≌△CBG(SAS),
∴AG=CG,∠FAG=∠BCG,
在△ABC中,∠GAC+∠ACG=∠ACB+∠BCG+∠GAC=∠ACB+∠BAG+∠GAC=∠ACB+∠BAC=180°-60°=120°,
∴∠AGC=180°-(∠GAC+∠ACG)=180°-120°=60°,
∴△AGC是等边三角形.


科目:初中数学 来源: 题型:
【题目】位于南开(融侨)中学旁边的“转转桥”是重庆市网红景点之一,在桥下人形天桥(如图1),其平面图如图2所示,天桥入口D点有一台阶DC,CD=0.5米,其坡度为i=1:0.75,在DC上方有一平层BC=1米,且BC与地面MN平行,在天桥顶端A点测得B点的俯角为63°,且AD⊥MN,为知道台阶AB的长度,请根据以上信息,帮小亮计算出台阶AB的长度,约为( )精确到0.1米,参考数据:sin63°≈0.90,cos63°≈0.45,tan63°≈2.00

A. 1.4米 B. 2.5米 C. 2.8米 D. 2.9米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() .规定“把点
.规定“把点![]() 先作关于
先作关于![]() 轴对称,再向左平移1个单位”为一次变化.经过第一次变换后,点
轴对称,再向左平移1个单位”为一次变化.经过第一次变换后,点![]() 的坐标为_______;经过第二次变换后,点
的坐标为_______;经过第二次变换后,点![]() 的坐标为_____;那么连续经过2019次变换后,点
的坐标为_____;那么连续经过2019次变换后,点![]() 的坐标为_______.
的坐标为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.二次函数y=ax2+bx+c(a≠0)的部分图象与x轴交于点A(﹣1,0),与y轴交于点B.且对称轴为x=1.则下面的四个结论:
①当x>﹣1时,y>0;
②一元二次方程ax2+bx+c=0的两根为x1=﹣1,x2=3;
③当y<0时,x<﹣1;
④抛物线上两点(x1,y1),(x2,y2).当x1>x2>2时,y1>y2
其中正确结论的个数是( )

A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
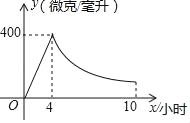
【题目】驾驶员血液中每毫升的酒精含量大于或等于200微克即为酒驾,某研究所经实验测得:成人饮用某品牌38度白酒后血液中酒精浓度y(微克/毫升)与饮酒时间x(小时)之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中酒精浓度上升和下降阶段y与x之间的函数表达式.
(2)问血液中酒精浓度不低于200微克/毫升的持续时间是多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
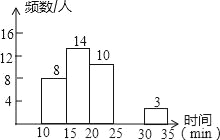
【题目】某校中午学生用餐比较拥挤,为建议学校分年级错时用餐,李老师带领数学学习小组在某天随机调查了部分学生,统计了他们从下课到就餐结束所用的时间,并绘制成统计表和如图所示的不完整统计图.
根据以上提供的信息,解答下列问题:
(1)表中a=_____,b=_____,c=_____,补全频数分布直方图;
(2)此次调查中,中位数所在的时间段是_____min.
时间分段/min | 频(人)数 | 百分比 |
10≤x<15 | 8 | 20% |
15≤x<20 | 14 | a |
20≤x<25 | 10 | 25% |
25≤x<30 | b | 12.50% |
30≤x<35 | 3 | 7.50% |
合计 | c | 100% |
(3)这所学校共有1200人,试估算从下课到就餐结束所用时间不少于20min的共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上,且
边上,且![]() 是射线
是射线![]() 上一动点(不与点
上一动点(不与点![]() 重合,且
重合,且![]() ),在射线
),在射线![]() 上截取
上截取![]() ,连接
,连接![]() .
.
![]() 当点
当点![]() 在线段
在线段![]() 上时,
上时,
①若点![]() 与点
与点![]() 重合时,请说明线段
重合时,请说明线段![]() ;
;
②如图2,若点![]() 不与点
不与点![]() 重合,请说明
重合,请说明![]() ;
;
![]() 当点
当点![]() 在线段
在线段![]() 的延长线上
的延长线上![]() 时,用等式表示线段
时,用等式表示线段![]() 之间的数量关系(直接写出结果,不需要证明).
之间的数量关系(直接写出结果,不需要证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
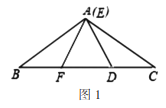
【题目】我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.

(1)概念理解:
如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是”等高底”三角形,请说明理由.
(2)问题探究:
如图2,△ABC是“等高底”三角形,BC是”等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连结AA′交直线BC于点D.若点B是△AA′C的重心,求![]() 的值.
的值.
(3)应用拓展:
如图3,已知l1∥l2,l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的![]() 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B和∠C的平分线交于点I,边AB和AC的垂直平分线交于点O,若∠BIC=90°+![]() θ,则∠BOC=( )
θ,则∠BOC=( )
A.90°﹣![]() θB.2θC.180°﹣θD.以上答案都不对
θB.2θC.180°﹣θD.以上答案都不对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com