
【题目】在△ABC中,∠B和∠C的平分线交于点I,边AB和AC的垂直平分线交于点O,若∠BIC=90°+![]() θ,则∠BOC=( )
θ,则∠BOC=( )
A.90°﹣![]() θB.2θC.180°﹣θD.以上答案都不对
θB.2θC.180°﹣θD.以上答案都不对
【答案】B
【解析】
根据角平分线的性质可得∠A=θ,再根据线段垂直平分线的性质和三角形内角和定理即可推出∠BOC.
解:如图,
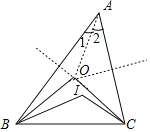
∵∠B和∠C的平分线交于点I,
∴∠IBC=![]() ∠ABC,∠ICB=
∠ABC,∠ICB=![]() ∠ACB,
∠ACB,
∠BIC=180°﹣(∠IBC+∠ICB)
=180°﹣![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
=180°﹣![]() (180°﹣∠BAC)
(180°﹣∠BAC)
=180°﹣90°+![]() ∠BAC
∠BAC
=90°+![]() ∠BAC,
∠BAC,
∵∠BIC=90°+![]() θ,
θ,
∴∠BAC=θ.
∵AB和AC的垂直平分线交于点O,
∴OA=OB=OC
∴∠1=∠OBA,∠2=∠OCA,
∴∠BOC=180°﹣(∠OBC+∠OCB)
=180°﹣(∠ABC﹣∠1+∠ACB﹣∠2)
=180°﹣(180°﹣∠BAC﹣∠1﹣∠2)
=∠BAC+∠1+∠2
=2∠BAC
=2θ.
故选:B.


科目:初中数学 来源: 题型:
【题目】在![]() ABCD中,∠ADC的平分线交直线BC于点E、交AB的延长线于点F,连接AC.
ABCD中,∠ADC的平分线交直线BC于点E、交AB的延长线于点F,连接AC.
(1)如图1,若∠ADC=90°,G是EF的中点,连接AG、CG.
①求证:BE=BF;
②请判断△AGC的形状,并说明理由.
(2)如图2,若∠ADC=60°,将线段FB绕点F顺时针旋转60°至FG,连接AG、CG,判断△AGC的形状.(直接写出结论不必证明)
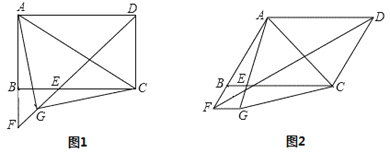
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.
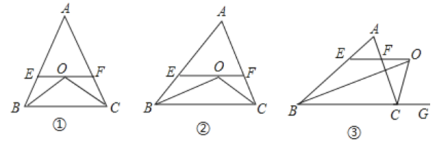
(1)图①中有几个等腰三角形?猜想:EF与BE、CF之间有怎样的关系.
(2)如图②,若AB≠AC,其他条件不变,图中还有等腰三角形吗?如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?
(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题:
汾河古称“汾”,又称汾水,是山西最大的河流,被山西人称为“母亲河”,对山西省的历史文化有着深远的影响.为打造“一川清水、两岸锦绣”的生态环境,现将一段长为![]() 的汾河两岸绿化任务交由甲、乙两个工程队先后接力完成.甲工程队每天绿化
的汾河两岸绿化任务交由甲、乙两个工程队先后接力完成.甲工程队每天绿化![]() ,乙工程队每天绿化
,乙工程队每天绿化![]() ,共用时
,共用时![]() 天.
天.
根据以上信息,小敏和小颖由自己的设想方案分别列出了尚不完整的方程组:
小敏: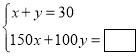
小颖: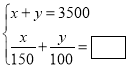

(1)请你在方框中补全小敏和小颖所列的方程组;
(2)根据小敏和小颖所列的方程组,分别指出未知数![]() ,
,![]() 表示的实际意义:
表示的实际意义:
小敏:![]() 表示_____________,
表示_____________,![]() 表示____________;
表示____________;
小颖:![]() 表示____________,
表示____________,![]() 表示______________;
表示______________;
(3)请你选择一种方案,求甲、乙两工程队分别绿化河岸多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其中红球有2个,黄球有1个,蓝球有1个.现有一张电影票,小明和小亮决定通过摸球游戏定输赢(赢的一方得电影票).游戏规则是:两人各摸1次球,先由小明从纸箱里随机摸出1个球,记录颜色后放回,将小球摇匀,再由小亮随机摸出1个球并记录颜色.若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏规则对双方公平吗?请你利用树状图或列表法说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形网格上有6个三角形:①△ABC;②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EFK.其中②~⑥中与①相似的是( )

A. ②③④ B. ③④⑤ C. ④⑤⑥ D. ②③⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
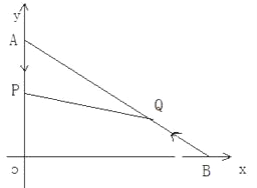
【题目】如图,在平面直角坐标系中,已知点A(0,12),B(16,0),动点P从点A开始在线段AO上以每秒1个单位的速度向点O移动,同时点Q从点B开始在BA上以每秒2个单位的速度向点A移动,设点P、Q移动的时间为t秒.
⑴求直线AB的解析式;
⑵求t为何值时,△APQ与△AOB相似?
⑶当t为何值时,△APQ的面积为![]() 个平方单位?
个平方单位?
⑷当t为何值时,△APQ的面积最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1.0,1.21,1.44,正放置的四个正方形的面积为S1、S2、S3、S4,则S1+S2+S3+S4= .
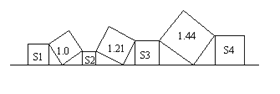
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场出售一批进价为2元的贺卡,在营运中发现此商品的日销价x(单位:元)与销售量y(单位:张)之间有如下关系:
x/元 | 3 | 4 | 5 | 6 |
y/张 | 20 | 15 | 12 | 10 |
(1)猜测并确定y与x的函数关系式.
(2)当日销售单价为10元时,贺卡的日销售量是多少张?
(3)设此卡的利润为W元,试求出W与x之间的函数关系式,若物价部门规定此卡的销售单价不能超过10元,试求出当日销售单价为多少元时,每天获得的利润最大并求出最大的利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com