
ЁОЬтФПЁПСаЗНГЬЃЈзщЃЉНтгІгУЬтЃК
ЗкКгЙХГЦЁАЗкЁБЃЌгжГЦЗкЫЎЃЌЪЧЩНЮїзюДѓЕФКгСїЃЌБЛЩНЮїШЫГЦЮЊЁАФИЧзКгЁБЃЌЖдЩНЮїЪЁЕФРњЪЗЮФЛЏгазХЩюдЖЕФгАЯьЃЎЮЊДђдьЁАвЛДЈЧхЫЎЁЂСНАЖНѕахЁБЕФЩњЬЌЛЗОГЃЌЯжНЋвЛЖЮГЄЮЊ![]() ЕФЗкКгСНАЖТЬЛЏШЮЮёНЛгЩМзЁЂввСНИіЙЄГЬЖгЯШКѓНгСІЭъГЩЃЎМзЙЄГЬЖгУПЬьТЬЛЏ
ЕФЗкКгСНАЖТЬЛЏШЮЮёНЛгЩМзЁЂввСНИіЙЄГЬЖгЯШКѓНгСІЭъГЩЃЎМзЙЄГЬЖгУПЬьТЬЛЏ![]() ЃЌввЙЄГЬЖгУПЬьТЬЛЏ
ЃЌввЙЄГЬЖгУПЬьТЬЛЏ![]() ЃЌЙВгУЪБ
ЃЌЙВгУЪБ![]() ЬьЃЎ
ЬьЃЎ
ИљОнвдЩЯаХЯЂЃЌаЁУєКЭаЁгБгЩздМКЕФЩшЯыЗНАИЗжБ№СаГіСЫЩаВЛЭъећЕФЗНГЬзщЃК
аЁУєЃК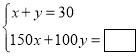
аЁгБЃК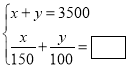

ЃЈ1ЃЉЧыФудкЗНПђжаВЙШЋаЁУєКЭаЁгБЫљСаЕФЗНГЬзщЃЛ
ЃЈ2ЃЉИљОнаЁУєКЭаЁгБЫљСаЕФЗНГЬзщЃЌЗжБ№жИГіЮДжЊЪ§![]() ЃЌ
ЃЌ![]() БэЪОЕФЪЕМЪвтвхЃК
БэЪОЕФЪЕМЪвтвхЃК
аЁУєЃК![]() БэЪО_____________ЃЌ
БэЪО_____________ЃЌ![]() БэЪО____________ЃЛ
БэЪО____________ЃЛ
аЁгБЃК![]() БэЪО____________ЃЌ
БэЪО____________ЃЌ![]() БэЪО______________ЃЛ
БэЪО______________ЃЛ
ЃЈ3ЃЉЧыФубЁдёвЛжжЗНАИЃЌЧѓМзЁЂввСНЙЄГЬЖгЗжБ№ТЬЛЏКгАЖЖрЩйУзЃП
ЁОД№АИЁПЃЈ1ЃЉаЁУєЃК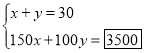 ЃЛаЁгБЃК
ЃЛаЁгБЃК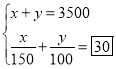 ЃЛЃЈ2ЃЉаЁУєЃКМзЙЄГЬЖгТЬЛЏКгАЖЕФЬьЪ§ЃЌввЙЄГЬЖгТЬЛЏКгАЖЕФЬьЪ§ЃЛаЁгБЃКМзЙЄГЬЖгТЬЛЏКгАЖЕФГЄЖШЃЌввЙЄГЬЖгТЬЛЏКгАЖЕФГЄЖШЃЛЃЈ3ЃЉМзЁЂввСНЙЄГЬЖгЗжБ№ТЬЛЏКгАЖ
ЃЛЃЈ2ЃЉаЁУєЃКМзЙЄГЬЖгТЬЛЏКгАЖЕФЬьЪ§ЃЌввЙЄГЬЖгТЬЛЏКгАЖЕФЬьЪ§ЃЛаЁгБЃКМзЙЄГЬЖгТЬЛЏКгАЖЕФГЄЖШЃЌввЙЄГЬЖгТЬЛЏКгАЖЕФГЄЖШЃЛЃЈ3ЃЉМзЁЂввСНЙЄГЬЖгЗжБ№ТЬЛЏКгАЖ![]() КЭ
КЭ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвзЕУаЁУєЩшxЮЊМзЙЄГЬЖгТЬЛЏКгАЖЕФЬьЪ§ЃЌyЮЊввЙЄГЬЖгТЬЛЏКгАЖЕФЬьЪ§ЃЎ
аЁгБЩшxЮЊМзЙЄГЬЖгТЬЛЏКгАЖЕФГЄЖШЃЌyЮЊввЙЄГЬЖгТЬЛЏКгАЖЕФГЄЖШЃЎЫљвдаЁУєЕФЗНГЬзщЮЊ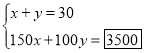 ЃЌаЁгБЕФЗНГЬзщЮЊ
ЃЌаЁгБЕФЗНГЬзщЮЊ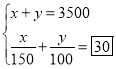 ЃЛ
ЃЛ
ЃЈ2ЃЉгЩx+y=30взЕУаЁУєЩшxЮЊМзЙЄГЬЖгТЬЛЏКгАЖЕФЬьЪ§ЃЌyЮЊввЙЄГЬЖгТЬЛЏКгАЖЕФЬьЪ§ЃЎ
гЩx+y=3500взЕУаЁгБЩшxЮЊМзЙЄГЬЖгТЬЛЏКгАЖЕФГЄЖШЃЌyЮЊввЙЄГЬЖгТЬЛЏКгАЖЕФГЄЖШЃЛ
ЃЈ3ЃЉШЮбЁвЛжжЗНАИЃЌНЋЗНГЬзщЧѓНтМДПЩ.
НтЃКЃЈ1ЃЉаЁУєЃК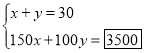 аЁгБЃК
аЁгБЃК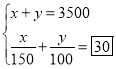
ЃЈ2ЃЉаЁУєЃКМзЙЄГЬЖгТЬЛЏКгАЖЕФЬьЪ§ЃЌввЙЄГЬЖгТЬЛЏКгАЖЕФЬьЪ§ЃЎ
аЁгБЃКМзЙЄГЬЖгТЬЛЏКгАЖЕФГЄЖШЃЌввЙЄГЬЖгТЬЛЏКгАЖЕФГЄЖШЃЎ
ЃЈ3ЃЉбЁдёЗНАИвЛЃКНтаЁУєЕФЗНГЬзщ![]() ЃЎ
ЃЎ
дЗНГЬзщПЩЛЏЮЊ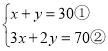 ЃЌ
ЃЌ
Ђй![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌЂл
ЃЌЂл
Ђк![]() ЂлЃЌЕУ
ЂлЃЌЕУ![]() ЃЌ
ЃЌ
Аб![]() ДњШыЂйЃЌЕУ
ДњШыЂйЃЌЕУ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
Д№ЃКМзЁЂввСНЙЄГЬЖгЗжБ№ТЬЛЏКгАЖ![]() КЭ
КЭ![]() ЃЎ
ЃЎ
бЁдёЗНАИЖўЃКНтаЁгБЕФЗНГЬзщ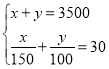 ЃЎ
ЃЎ
дЗНГЬзщПЩЛЏЮЊ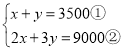
Ђй![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌЂл
ЃЌЂл
Ђк![]() ЂлЃЌЕУ
ЂлЃЌЕУ![]() ЃЌАб
ЃЌАб![]() ДњШыЂйЃЌЕУ
ДњШыЂйЃЌЕУ![]() ЃЎ
ЃЎ
Д№ЃКМзЁЂввСНЙЄГЬЖгЗжБ№ТЬЛЏКгАЖ![]() КЭ
КЭ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЎЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФВПЗжЭМЯѓгыxжсНЛгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌгыyжсНЛгкЕуBЃЎЧвЖдГЦжсЮЊx=1ЃЎдђЯТУцЕФЫФИіНсТлЃК
ЂйЕБxЃОЉ1ЪБЃЌyЃО0ЃЛ
ЂквЛдЊЖўДЮЗНГЬax2+bx+c=0ЕФСНИљЮЊx1=Љ1ЃЌx2=3ЃЛ
ЂлЕБyЃМ0ЪБЃЌxЃМЉ1ЃЛ
ЂмХзЮяЯпЩЯСНЕуЃЈx1ЃЌy1ЃЉЃЌЃЈx2ЃЌy2ЃЉЃЎЕБx1ЃОx2ЃО2ЪБЃЌy1ЃОy2
Цфжае§ШЗНсТлЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ

A. 3 B. 2 C. 1 D. 0
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧЖЈвхЃКШчЙћвЛИіШ§НЧаЮвЛЬѕБпЩЯЕФИпЕШгкетЬѕБпЃЌФЧУДетИіШ§НЧаЮНазіЁАЕШИпЕзЁБШ§НЧаЮЃЌетЬѕБпНазіетИіШ§НЧаЮЕФЁАЕШЕзЁБЃЎ

ЃЈ1ЃЉИХФюРэНтЃК
ШчЭМ1ЃЌдкЁїABCжаЃЌAC=6ЃЌBC=3ЃЌЁЯACB=30ЁуЃЌЪдХаЖЯЁїABCЪЧЗёЪЧЁБЕШИпЕзЁБШ§НЧаЮЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ2ЃЉЮЪЬтЬНОПЃК
ШчЭМ2ЃЌЁїABCЪЧЁАЕШИпЕзЁБШ§НЧаЮЃЌBCЪЧЁБЕШЕзЁБЃЌзїЁїABCЙигкBCЫљдкжБЯпЕФЖдГЦЭМаЮЕУЕНЁїA'BCЃЌСЌНсAAЁфНЛжБЯпBCгкЕуDЃЎШєЕуBЪЧЁїAAЁфCЕФжиаФЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЃЈ3ЃЉгІгУЭиеЙЃК
ШчЭМ3ЃЌвбжЊl1ЁЮl2ЃЌl1гыl2жЎМфЕФОрРыЮЊ2ЃЎЁАЕШИпЕзЁБЁїABCЕФЁАЕШЕзЁБBCдкжБЯпl1ЩЯЃЌЕуAдкжБЯпl2ЩЯЃЌгавЛБпЕФГЄЪЧBCЕФ![]() БЖЃЎНЋЁїABCШЦЕуCАДЫГЪБеыЗНЯђа§зЊ45ЁуЕУЕНЁїA'B'CЃЌAЁфCЫљдкжБЯпНЛl2гкЕуDЃЎЧѓCDЕФжЕЃЎ
БЖЃЎНЋЁїABCШЦЕуCАДЫГЪБеыЗНЯђа§зЊ45ЁуЕУЕНЁїA'B'CЃЌAЁфCЫљдкжБЯпНЛl2гкЕуDЃЎЧѓCDЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
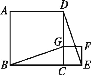
ЁОЬтФПЁПШчЭМ,B,C,EЪЧЭЌвЛжБЯпЩЯЕФШ§ИіЕу,ЫФБпаЮABCDгыЫФБпаЮCEFGЖМЪЧе§ЗНаЮ.СЌНгBG,DE.
(1)ЙлВьВТЯыBGгыDEжЎМфЕФДѓаЁЙиЯЕ,ВЂжЄУїФуЕФНсТл.
(2)ЭМжаЪЧЗёДцдкЭЈЙ§а§зЊФмЙЛЛЅЯржиКЯЕФСНИіШ§НЧаЮ?ШєДцдк,ЧыжИГі,ВЂЫЕГіа§зЊЙ§ГЬ;ШєВЛДцдк,ЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСаЁЧПЭЌбЇЪ§бЇзївЕБОЩЯЕФНиЭМФкШнВЂЭъГЩШЮЮёЃК
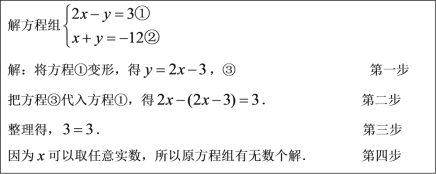
ШЮЮёЃК
ЃЈ1ЃЉетжжНтЗНГЬзщЕФЗНЗЈГЦЮЊ_____________ЃЛ
ЃЈ2ЃЉРћгУДЫЗНЗЈНтЗНГЬзщЕФЙ§ГЬжаЫљЬхЯжЕФЪ§бЇЫМЯыЪЧ____________ЃЛЃЈЧыФуЬюаДе§ШЗбЁЯюЃЉ
AЃЎзЊЛЏЫМЯы BЃЎКЏЪ§ЫМЯы CЃЎЪ§аЮНсКЯЫМЯы DЃЎЙЋРэЛЏЫМЯы
ЃЈ3ЃЉаЁЧПЕФНтЗЈе§ШЗТ№ЃПШчЙћВЛе§ШЗЃЌДэдкФФвЛВНЃПЧыФуЧѓГіе§ШЗЕФНтЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГЌЪаМЦЛЎдкЁАЪЎжмФъЁБЧьЕфЕБЬьПЊеЙЙКЮяГщНБЛюЖЏ,ЗВЕБЬьдкИУГЌЪаЙКЮяЕФЙЫПЭ,ОљгавЛДЮГщНБЕФЛњЛс,ГщНБЙцдђШчЯТ:ШчЭМ,НЋдВаЮзЊХЬЦНОљЗжГЩЫФИіЩШаЮ,ЗжБ№БъЩЯ1,2,3,4ЫФИіЪ§зж,ГщНБепСЌајзЊЖЏзЊХЬСНДЮ,ЕБУПДЮзЊХЬЭЃжЙКѓжИеыЫљжИЩШаЮФкЕФЪ§зжЮЊУПДЮЫљЕУЕФЪ§(ШєжИеыжИдкЗжНчЯпЪБжизЊ);ЕБСНДЮЫљЕУЪ§зжжЎКЭЮЊ8ЪБ,ЗЕЯжН№20дЊ;ЕБСНДЮЫљЕУЪ§зжжЎКЭЮЊ7ЪБ,ЗЕЯжН№15дЊ;ЕБСНДЮЫљЕУЪ§зжжЎКЭЮЊ6ЪБ,ЗЕЯжН№10дЊ.ФГЙЫПЭВЮМгвЛДЮГщНБ,ФмЛёЕУЗЕЛЙЯжН№ЕФИХТЪЪЧ(ЁЁЁЁ)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌЁЯBКЭЁЯCЕФЦНЗжЯпНЛгкЕуIЃЌБпABКЭACЕФДЙжБЦНЗжЯпНЛгкЕуOЃЌШєЁЯBICЃН90Ёу+![]() ІШЃЌдђЁЯBOCЃНЃЈ ЃЉ
ІШЃЌдђЁЯBOCЃНЃЈ ЃЉ
A.90ЁуЉ![]() ІШB.2ІШC.180ЁуЉІШD.вдЩЯД№АИЖМВЛЖд
ІШB.2ІШC.180ЁуЉІШD.вдЩЯД№АИЖМВЛЖд
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЫЮчНкЪЧЮвЙњЕФДЋЭГНкШеЃЌШЫУЧЫигаГдєезгЕФЯАЫзЃЌФГЩЬГЁдкЖЫЮчНкРДСйжЎМЪгУ3000дЊЙКНј![]() ЁЂ
ЁЂ![]() СНжжєезг1100ИіЃЌЙКТђ
СНжжєезг1100ИіЃЌЙКТђ![]() жжєезггыЙКТђ
жжєезггыЙКТђ![]() жжєезгЕФЗбгУЯрЭЌЃЌвбжЊ
жжєезгЕФЗбгУЯрЭЌЃЌвбжЊ![]() єезгЕФЕЅМлЪЧ
єезгЕФЕЅМлЪЧ![]() жжєезгЕЅМлЕФ1.2БЖ.
жжєезгЕЅМлЕФ1.2БЖ.
ЃЈ1ЃЉЧѓ![]() ЁЂ
ЁЂ![]() СНжжєезгЕФЕЅМлИїЪЧЖрЩйЃП
СНжжєезгЕФЕЅМлИїЪЧЖрЩйЃП
ЃЈ2ЃЉШєМЦЛЎгУВЛГЌЙ§7000дЊЕФзЪН№дйДЮЙКТђ![]() ЁЂ
ЁЂ![]() СНжжєезгЙВ2600ИіЃЌвбжЊ
СНжжєезгЙВ2600ИіЃЌвбжЊ![]() ЁЂ
ЁЂ![]() СНжжєезгЕФНјМлВЛБфЃЌЧѓ
СНжжєезгЕФНјМлВЛБфЃЌЧѓ![]() жаєезгзюЖрФмЙКНјЖрЩйИіЃП
жаєезгзюЖрФмЙКНјЖрЩйИіЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГвЉГЇЯњЪлВПУХИљОнЪаГЁЕїбаНсЙћЃЌЖдИУГЇЩњВњЕФвЛжжаТаЭдСЯвЉЮДРДСНФъЕФЯњЪлНјаадЄВтЃЌОЎНЈСЂШчЯТФЃаЭЃКЩшЕкtИідТИУдСЯвЉЕФдТЯњЪлСПЮЊPЃЈЕЅЮЛЃКЖжЃЉЃЌPгыtжЎМфДцдкШчЭМЫљЪОЕФКЏЪ§ЙиЯЕЃЌЦфЭМЯѓЪЧКЏЪ§P=![]() ЃЈ0ЃМtЁм8ЃЉЕФЭМЯѓгыЯпЖЮABЕФзщКЯЃЛЩшЕкtИідТЯњЪлИУдСЯвЉУПЖжЕФУЋРћШѓЮЊQЃЈЕЅЮЛЃКЭђдЊЃЉЃЌQгыtжЎМфТњзуШчЯТЙиЯЕЃКQ=
ЃЈ0ЃМtЁм8ЃЉЕФЭМЯѓгыЯпЖЮABЕФзщКЯЃЛЩшЕкtИідТЯњЪлИУдСЯвЉУПЖжЕФУЋРћШѓЮЊQЃЈЕЅЮЛЃКЭђдЊЃЉЃЌQгыtжЎМфТњзуШчЯТЙиЯЕЃКQ=![]()
ЃЈ1ЃЉЕБ8ЃМtЁм24ЪБЃЌЧѓPЙигкtЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЩшЕкtИідТЯњЪлИУдСЯвЉЕФдТУЋРћШѓЮЊwЃЈЕЅЮЛЃКЭђдЊЃЉ
ЂйЧѓwЙигкtЕФКЏЪ§НтЮіЪНЃЛ
ЂкИУвЉГЇЯњЪлВПУХЗжЮіШЯЮЊЃЌ336ЁмwЁм513ЪЧзюгаРћгкИУдСЯвЉПЩГжајЩњВњКЭЯњЪлЕФдТУЋРћШѓЗЖЮЇЃЌЧѓДЫЗЖЮЇЫљЖдгІЕФдТЯњЪлСПPЕФзюаЁжЕКЭзюДѓжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com