
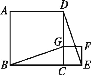
【题目】如图,B,C,E是同一直线上的三个点,四边形ABCD与四边形CEFG都是正方形.连接BG,DE.
(1)观察猜想BG与DE之间的大小关系,并证明你的结论.
(2)图中是否存在通过旋转能够互相重合的两个三角形?若存在,请指出,并说出旋转过程;若不存在,请说明理由.
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
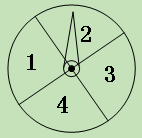
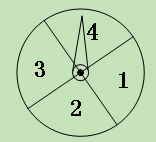
【题目】(11·孝感)学生甲与学生乙玩一种转盘游戏.如图是两个完全相同的转盘,每个转盘被分成面积相等的四个区域,分别用数字“1”、“2”、“3”、“4”表示.固定指针,同时转动两个转盘,任其自由停止,若两指针所指数字的积为奇数,则甲获胜;若两指针所指数字的积为偶数,则乙获胜;若指针指向扇形的分界线,则都重转一次.在该游戏中乙获胜的概率是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
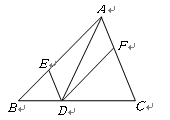
【题目】如图,在![]() 中,点D、E、F分别在边
中,点D、E、F分别在边![]() 、
、![]() 、
、![]() 上,且
上,且![]() ,
,![]() .下列四种说法:
.下列四种说法:
①四边形![]() 是平行四边形;②如果
是平行四边形;②如果![]() ,那么四边形
,那么四边形![]() 是矩形;
是矩形;
③如果![]() 平分
平分![]() ,那么四边形
,那么四边形![]() 是菱形;
是菱形;
④如果![]() 且
且![]() ,那么四边形
,那么四边形![]() 是菱形.
是菱形.
其中,正确的有 .(只填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.
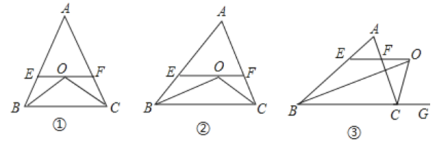
(1)图①中有几个等腰三角形?猜想:EF与BE、CF之间有怎样的关系.
(2)如图②,若AB≠AC,其他条件不变,图中还有等腰三角形吗?如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?
(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
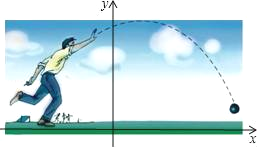
【题目】如图,一名男生推铅球,铅球行进的高度y(m)与水平距离x(m)之间的关系是二次函数的关系.铅球行进起点的高度为![]() m,行进到水平距离为4m时达到最高处,最大高度为3m.
m,行进到水平距离为4m时达到最高处,最大高度为3m.
(1)求二次函数的解析式(化成一般形式);
(2)求铅球推出的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题:
汾河古称“汾”,又称汾水,是山西最大的河流,被山西人称为“母亲河”,对山西省的历史文化有着深远的影响.为打造“一川清水、两岸锦绣”的生态环境,现将一段长为![]() 的汾河两岸绿化任务交由甲、乙两个工程队先后接力完成.甲工程队每天绿化
的汾河两岸绿化任务交由甲、乙两个工程队先后接力完成.甲工程队每天绿化![]() ,乙工程队每天绿化
,乙工程队每天绿化![]() ,共用时
,共用时![]() 天.
天.
根据以上信息,小敏和小颖由自己的设想方案分别列出了尚不完整的方程组:
小敏: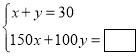
小颖: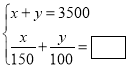

(1)请你在方框中补全小敏和小颖所列的方程组;
(2)根据小敏和小颖所列的方程组,分别指出未知数![]() ,
,![]() 表示的实际意义:
表示的实际意义:
小敏:![]() 表示_____________,
表示_____________,![]() 表示____________;
表示____________;
小颖:![]() 表示____________,
表示____________,![]() 表示______________;
表示______________;
(3)请你选择一种方案,求甲、乙两工程队分别绿化河岸多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形网格上有6个三角形:①△ABC;②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EFK.其中②~⑥中与①相似的是( )

A. ②③④ B. ③④⑤ C. ④⑤⑥ D. ②③⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y=![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和y=![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com