
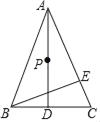
【题目】如图,△ABC中,AB=AC=13,BC=10,AD⊥BC,BE⊥AC,P为AD上一动点,则PE+PC的最小值为__________.
【答案】![]()
【解析】
根据题意作E关于AD的对称点M,连接CM交AD于P,连接EF,过C作CN⊥AB于N,根据三线合一定理求出BD的长和AD⊥BC,根据勾股定理求出AD,根据三角形面积公式求出CN,根据对称性质求出CP+EP=CM,根据垂线段最短得出CP+EP≥![]() ,即可得出答案.
,即可得出答案.
作E关于AD的对称点M,连接CM交AD于P,连接EP,过C作CN⊥AB于N,
∵AB=AC=13,BC=10,AD是BC边上的中线,
∴BD=DC=5,AD⊥BC,AD平分∠BAC,
∴M在AB上,
在Rt△ABD中,由勾股定理得:AD=![]() =12,
=12,
∴S△ABC=![]() ×BC×AD=
×BC×AD=![]() ×AB×CN,
×AB×CN,
∴CN=![]() =
=![]() ,
,
∵E关于AD的对称点M,
∴EP=PM,
∴CP+EP=CP+PM=CM,
根据垂线段最短得出:CM≥CN,
即CP+EP≥![]() ,
,
即CP+EP的最小值是![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】某学校为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行八百米跑体能测试,测试结果分为A、B、C、D四个等级,请根据两幅统计图中的信息回答下列题:
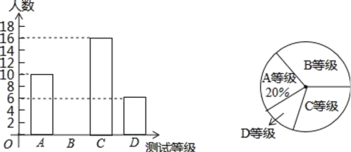
(1)本次调查活动采取了 的调查方式.(填“普查”或“抽样调查”)
(2)本次调查共调查了________人,图(2)中选项C的圆心角为 ______度.
(3)求本次测试结果为B等级的学生数,并补全条形统计图;
(4)若该中学八年级共有900名学生,请你估计八年级学生中体能测试结果为D等级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.二次函数y=ax2+bx+c(a≠0)的部分图象与x轴交于点A(﹣1,0),与y轴交于点B.且对称轴为x=1.则下面的四个结论:
①当x>﹣1时,y>0;
②一元二次方程ax2+bx+c=0的两根为x1=﹣1,x2=3;
③当y<0时,x<﹣1;
④抛物线上两点(x1,y1),(x2,y2).当x1>x2>2时,y1>y2
其中正确结论的个数是( )

A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
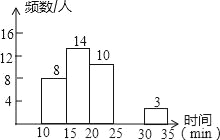
【题目】某校中午学生用餐比较拥挤,为建议学校分年级错时用餐,李老师带领数学学习小组在某天随机调查了部分学生,统计了他们从下课到就餐结束所用的时间,并绘制成统计表和如图所示的不完整统计图.
根据以上提供的信息,解答下列问题:
(1)表中a=_____,b=_____,c=_____,补全频数分布直方图;
(2)此次调查中,中位数所在的时间段是_____min.
时间分段/min | 频(人)数 | 百分比 |
10≤x<15 | 8 | 20% |
15≤x<20 | 14 | a |
20≤x<25 | 10 | 25% |
25≤x<30 | b | 12.50% |
30≤x<35 | 3 | 7.50% |
合计 | c | 100% |
(3)这所学校共有1200人,试估算从下课到就餐结束所用时间不少于20min的共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上,且
边上,且![]() 是射线
是射线![]() 上一动点(不与点
上一动点(不与点![]() 重合,且
重合,且![]() ),在射线
),在射线![]() 上截取
上截取![]() ,连接
,连接![]() .
.
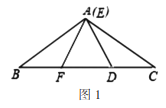
![]() 当点
当点![]() 在线段
在线段![]() 上时,
上时,
①若点![]() 与点
与点![]() 重合时,请说明线段
重合时,请说明线段![]() ;
;
②如图2,若点![]() 不与点
不与点![]() 重合,请说明
重合,请说明![]() ;
;
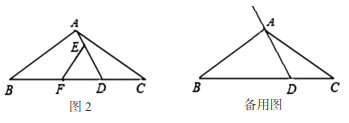
![]() 当点
当点![]() 在线段
在线段![]() 的延长线上
的延长线上![]() 时,用等式表示线段
时,用等式表示线段![]() 之间的数量关系(直接写出结果,不需要证明).
之间的数量关系(直接写出结果,不需要证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
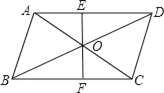
【题目】如图平行四边形ABCD中,对角线AC,BD交于点O,EF过点O,并与AD,BC分别交于点E,F,已知AE=3,BF=5
(1)求BC的长;
(2)如果两条对角线长的和是20,求三角形△AOD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.

(1)概念理解:
如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是”等高底”三角形,请说明理由.
(2)问题探究:
如图2,△ABC是“等高底”三角形,BC是”等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连结AA′交直线BC于点D.若点B是△AA′C的重心,求![]() 的值.
的值.
(3)应用拓展:
如图3,已知l1∥l2,l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的![]() 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
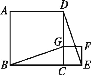
【题目】如图,B,C,E是同一直线上的三个点,四边形ABCD与四边形CEFG都是正方形.连接BG,DE.
(1)观察猜想BG与DE之间的大小关系,并证明你的结论.
(2)图中是否存在通过旋转能够互相重合的两个三角形?若存在,请指出,并说出旋转过程;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进![]() 、
、![]() 两种粽子1100个,购买
两种粽子1100个,购买![]() 种粽子与购买
种粽子与购买![]() 种粽子的费用相同,已知
种粽子的费用相同,已知![]() 粽子的单价是
粽子的单价是![]() 种粽子单价的1.2倍.
种粽子单价的1.2倍.
(1)求![]() 、
、![]() 两种粽子的单价各是多少?
两种粽子的单价各是多少?
(2)若计划用不超过7000元的资金再次购买![]() 、
、![]() 两种粽子共2600个,已知
两种粽子共2600个,已知![]() 、
、![]() 两种粽子的进价不变,求
两种粽子的进价不变,求![]() 中粽子最多能购进多少个?
中粽子最多能购进多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com