
如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,∠1=∠2.
(1)求证:BE=DF;
(2)求证:AF∥CE.


【考点】平行四边形的判定与性质;全等三角形的判定与性质.
【分析】(1)利用平行四边形的性质得出∠5=∠3,∠AEB=∠4,进而利用全等三角形的判定得出即可;
(2)利用全等三角形的性质得出AE=CF,进而得出四边形AECF是平行四边形,即可得出答案.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠5=∠3,
∵∠1=∠2,
∴∠AEB=∠4,
在△ABE和△CDF中,

 ,
,
∴△ABE≌△CDF(AAS),
∴BE=DF;
(2)由(1)得△ABE≌△CDF,
∴AE=CF,
∵∠1=∠2,
∴AE∥CF,
∴四边形AECF是平行四边形,
∴AF∥CE.




 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图.
根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图;
(2)求扇形统计图中m的值和“E”组对应的圆心角度数;
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数.


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,直线y=﹣3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,点D在双曲线
 (k≠0)上.将正方形沿x轴负方向平移a个单位长度后,点C恰好落在该双曲线上,则a的值是( )
(k≠0)上.将正方形沿x轴负方向平移a个单位长度后,点C恰好落在该双曲线上,则a的值是( )


A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
.下列命题中,真命题是( )
A.四边相等的四边形是正方形
B.对角线相等的菱形是正方形
C.正方形的两条对角线相等,但不互相垂直平分
D.矩形、菱形、正方形都具有“对角线相等”的性质
查看答案和解析>>
科目:初中数学 来源: 题型:
一只不透明的袋子中有2个红球,3个绿球和5个白球,每个球除颜色外都相同,将球搅匀,从中任意摸出一个球.
(1)会有哪些可能的结果?
(2)你认为摸到哪种颜色的球的可能性最大?哪种颜色的球的可能性最小?
查看答案和解析>>
科目:初中数学 来源: 题型:
某学校为了解本校学生课外阅读的情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成统计表.已知该校全体学生人数为1200人,由此可以估计每周课外阅读时间在1~2(不含1)小时的学生有 人.
| 每周课外阅读时间(小时) | 0~1 | 1~2 (不含1) | 2~3 (不含2) | 超过3 |
| 人 数 | 7 | 10 | 14 | 19 |
查看答案和解析>>
科目:初中数学 来源: 题型:
“低碳环保,你我同行”.两年来,扬州市区的公共自行车给市民出行带来切实方便.电视台记者在某区街头随机选取了市民进行调查,调查的问题是“您大概多久使用一次公共自行车?”,将本次调查结果归为四种情况:A.每天都用;B.经常使用;C.偶尔使用;D.从未使用.将这次调查情况整理并绘制如下两幅统计图如图2:


根据图中的信息,解答下列问题:
(1)本次活动共有 位市民参与调查;
(2)补全条形统计图和扇形统计图;
(3)扇形统计图中A项所对应的圆心角的度数为
(4)根据统计结果,若该区有46万市民,请估算每天都用公共自行车的市民约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
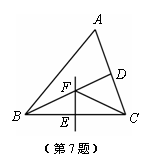
如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连结CF.若∠A=60°,∠ACF =45°,则∠ABC的度数为( )
 A.45° B.50° C.55° D.60°
A.45° B.50° C.55° D.60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com