
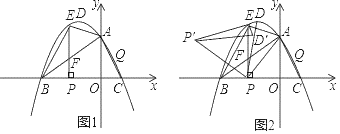
【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() +2与x轴交于B、C两点,与y轴交于点A,抛物线的顶点为D.连接AB,点E是第二象限内的抛物线上的一动点,过点E作EP⊥BC于点P,交线段AB于点F.
+2与x轴交于B、C两点,与y轴交于点A,抛物线的顶点为D.连接AB,点E是第二象限内的抛物线上的一动点,过点E作EP⊥BC于点P,交线段AB于点F.
(1)连接EA、EB,取线段AC的中点Q,当△EAB面积最大时,在x轴上找一点R使得|RE一RQ|值最大,请求出R点的坐标及|RE﹣RQ|的最大值;
(2)如图2,在(1)的条件下,将△PED绕E点旋转得△ED′P′,当△AP′P是以AP为直角边的直角三角形时,求点P′的坐标.
【答案】(1)![]() (2)当△AP′P是以AP为直角边的直角三角形时,点P′的坐标为(
(2)当△AP′P是以AP为直角边的直角三角形时,点P′的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)先求直线AB解析式,设点E横坐标为e,则能用e表示E、F的坐标进而表示EF,求得△EAB面积是关于e的二次函数,易得e=﹣![]() 时△EAB面积最大,进而得E的坐标.由三角形两边之差小于第三边可知,当E、Q、R成一直线时,|RE﹣RQ|=EQ最大;由Q为AC中点求得Q坐标,求直线EQ解析式即能求EQ与x轴的交点R坐标及EQ的长.
时△EAB面积最大,进而得E的坐标.由三角形两边之差小于第三边可知,当E、Q、R成一直线时,|RE﹣RQ|=EQ最大;由Q为AC中点求得Q坐标,求直线EQ解析式即能求EQ与x轴的交点R坐标及EQ的长.
(2)设P'坐标为(m、n),由于不确定以点A还是点P为直角顶点,故需分两类情况讨论.每种情况下都易得有关P'、P的三角形与△AOP相似,由对应边成比例列得关于m、n的二元方程;又由旋转得EP'=EP=![]() ,根据勾股定理又列得关于m、n的二元方程,联立两二元方程组即求出m、n的值.
,根据勾股定理又列得关于m、n的二元方程,联立两二元方程组即求出m、n的值.
(1)∵y=0时,﹣![]() +2=0,解得:x1=﹣3,x2=1,
+2=0,解得:x1=﹣3,x2=1,
∴B(﹣3,0),C(1,0),
∵x=0时,y=2,,
∴A(0,2),
设直线AB的解析式为y=kx+b,
∴![]() 解得:
解得:![]() ,
,
∴直线AB的解析式为:y=![]() x+2,
x+2,
设点E(e,﹣![]() e2﹣
e2﹣![]() e+2),则点F(e,
e+2),则点F(e,![]() e+2),
e+2),
∴EF=﹣![]() e2﹣
e2﹣![]() e+2﹣(
e+2﹣(![]() e+2)=﹣
e+2)=﹣![]() e2﹣2e
e2﹣2e
∴S△EAB=![]() OBEF=
OBEF=![]() ×3(﹣
×3(﹣![]() e2﹣2e)=﹣e2﹣3e=﹣(e+
e2﹣2e)=﹣e2﹣3e=﹣(e+![]() )2+
)2+![]() ,
,
∵﹣3<e<0
∴当e=﹣![]() 时,△EAB的面积最大,
时,△EAB的面积最大,
∴﹣![]() e2﹣
e2﹣![]() e+2=
e+2=![]() ,
,
∴此时点E坐标为(-![]() ,
,![]() )
)
如图1,
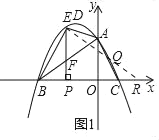
连接并延长EQ,交x轴于点R,则此时|RE﹣RQ|=EQ值最大
∵Q是AC中点,
∴Q(![]() ,1)
,1)
设直线EQ解析式为:y=ax+c,
∴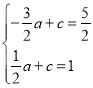 ,解得:
,解得: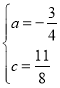 ,
,
∴直线EQ解析式为:y=![]() x+
x+![]() ,
,
当y=0时,![]() x+
x+![]() =0,解得:x=
=0,解得:x=![]() ,
,
∴R(![]() ,0),
,0),
此时|RE﹣RQ|的最大值EQ=![]() ,
,
(2)设点P'坐标为(m,n)
∵EP⊥x轴,E(-![]() ,
,![]() )
)
∴P(-![]() ,0),EP=
,0),EP=![]() ,AP=
,AP=![]() ,
,
i)当∠P'PA=90°时,如图2,
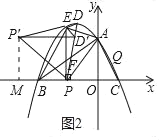
过点P'作P'M⊥x轴于点M,
∴∠P'MP=∠POA=90°,∠PP'M+∠P'PM=∠P'PM+∠APO=90°,
∴∠PP'M=∠APO,
∴△PP'M∽△APO,
∴![]() ,即:
,即: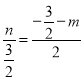 ,
,
整理得:4n+3m=![]() ①,
①,
∵EP'=EP
∴(m+![]() )2+(n﹣
)2+(n﹣![]() )2=(
)2=(![]() )2②,
)2②,
联立①②解方程组得: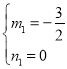 (舍去)
(舍去)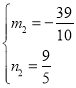 ,
,
∴P'(![]() ,
,![]() );
);
ii)当∠PAP'=90°时,如图3,过点P'作P'N⊥y轴于点N;
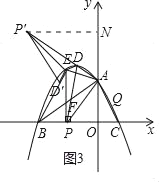
由△P'AN∽△APO得![]() ,即:
,即: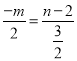 ,
,
整理得:3m+4n=8①,
∵EP'=EP,
∴(m+![]() )2+(n﹣
)2+(n﹣![]() )2=(
)2=(![]() )2②,
)2②,
联立①②解方程组得: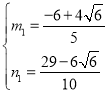 ,
,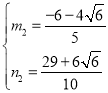 ,
,
∴P'(![]() ,
,![]() )或(
)或(![]() ,
,![]() ),
),
综上所述,当△AP′P是以AP为直角边的直角三角形时,点P′的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)


科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,抛物线y=-![]() x2-
x2-![]() x-3交x轴于A、B两点(点A在点B的左侧),交y轴于点C.
x-3交x轴于A、B两点(点A在点B的左侧),交y轴于点C.

(1)求直线AC的解析式;
(2)①点P是直线AC上方抛物线上的一个动点(不与点A、点C重合),过点P作PD⊥AC于点D,求PD的最大值;
②当线段PD的长度最大时,点Q从点P出发,先以每秒1个单位长度的速度沿适当的路径运动到y轴上的点M处,再沿MC以每秒![]() 个单位长度的速度运动到点C停止,当点Q在整个运动过程中用时最少时,求点M的坐标;
个单位长度的速度运动到点C停止,当点Q在整个运动过程中用时最少时,求点M的坐标;
(3)如图②,将△BOC沿直线BC平移,点B平移后的对应点为点B',点O平移后的对应点为点O',点C平移后的对应点为点C',点S是坐标平面内一点,若以A、C、O'、S为顶点的四边形是菱形,求出所有符合条件的点O'的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.

(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小刚一起做游戏,游戏规则如下:将分别标有数字 1, 2, 3, 4 的 4 个小球放入一个不透明的袋子中,这些球除数字外都相同.从中随机摸出一个球记下数字后放回,再从中随机摸出一个球记下数字.若两次数字差的绝对值小于 2,则小明获胜,否则小刚获胜.这个游戏对两人公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
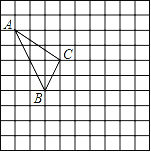
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)点B′的坐标为 .
(4)△ABC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学围绕“哈尔滨市周边五大名山,即:香炉山、凤凰山、金龙山、帽儿山、二龙山,你最喜欢那一座山?(每名学生必选且只选一座山)的问题在全校范围内随机抽取了部分学生进行问卷调查,根据调查结果绘制了如图的不完整的统计图:
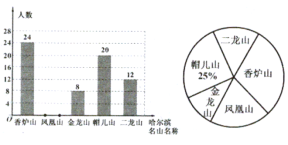
(1)求本次调查的样本容量;
(2)求本次调查中,最喜欢凤凰山的学生人数,并补全条形统计图;
(3)若该中学共有学生1200人,请你估计该中学最喜欢香炉山的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用电,某市对居民用电实行“阶梯收费”(总电费=第一阶梯电费+第二阶梯电费).规定:用电量不超过200度按第一阶梯电价收费,超过200度的部分按第二阶梯电价收费,如图是张磊家2018年2月和3月所交电费的收据.
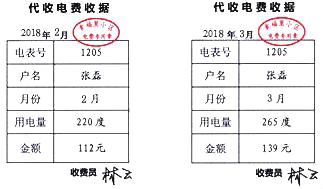
(1)该市规定的第一阶梯电价和第二阶梯电价单价分别为多少?
(2)张磊家4月份家庭支出计划中电费为160元,他家最大用电量为多少度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com