
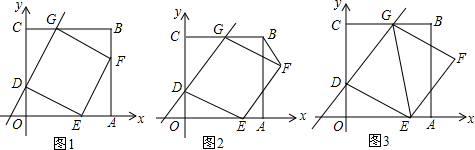
分析 (1)将x=0代入y=mx+2得y=2,故此点D的坐标为(0,2),由CG=OD=2可知点G的坐标为(2,6),将点G(2,6)代入y=mx+2可求得m=2;
(2)①如图1所示:过点F作FH⊥BC,垂足为H,延长FG交y轴与点N.先证明Rt△GHF≌Rt△EOD,从而得到FH=DO=2,由三角形的面积公式可知:S=6-a.②当s=1时,a=5,在△CGD中由勾股定理可求得DG=$\sqrt{41}$,由菱形的性质可知;DG=DE=$\sqrt{41}$,在Rt△DOE中由勾股定理可求得OE=$\sqrt{37}$>6,故S≠1;
(3)如图2所示:连接DF交EG于点M,过点M作MN⊥y轴,垂足为N.由菱形的性质可知:DM⊥GM,点M为DF的中点,根据角平分线的性质可知:MD=CD=4,由中点坐标公式可知点M的纵坐标为3,于是得到ND=1,根据勾股定理可求得MN=$\sqrt{15}$,于是得到点M的坐标为($\sqrt{15}$,3)然后利用待定系数法求得DM、GM的解析式,从而可得到点G的坐标,最后将点G的坐标代入y=mx+2可求得m=$\frac{\sqrt{15}}{3}$.
解答 (1)∵将x=0代入y=mx+2得;y=2,
∴点D的坐标为(0,2).
∵CG=OD=2,
∴点G的坐标为(2,6).
将点G(2,6)代入y=mx+2得:2m+2=6.
解得:m=2.
∴直线DG的函数表达式为y=2x+2.
(2)①如图1所示:过点F作FH⊥BC,垂足为H,延长FG交y轴与点N.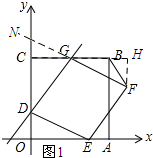
∵四边形DEFG为菱形,
∴GF=DE,GF∥DE.
∴∠GNC=∠EDO.
∴∠NGC=∠DEO.
∴∠HGF=∠DEO.
在Rt△GHF和Rt△EOD中,
$\left\{\begin{array}{l}{∠HGF=∠DEO}\\{∠GHF=∠EOD}\\{DE=FG}\end{array}\right.$,
∴Rt△GHF≌Rt△EOD.
∴FH=DO=2.
∴${S}_{△GBF}=\frac{1}{2}GB•HF$=$\frac{1}{2}$×2×(6-a)=6-a.
∴S与a之间的函数关系式为:S=6-a.
②当s=1时,则6-a=1.
解得:a=5.
∴点G的坐标为(5,6).
在△DCG中,由勾股定理可知;DG=$\sqrt{C{D}^{2}+C{G}^{2}}$=$\sqrt{{4}^{2}+{5}^{2}}$=$\sqrt{41}$.
∵四边形GDEF是菱形,
∴DE=DG=$\sqrt{41}$.
在Rt△DOE中,由勾股定理可知OE=$\sqrt{D{E}^{2}-O{D}^{2}}$=$\sqrt{41-4}$=$\sqrt{37}$>6.
∴OE>OA.
∴点E不在OA上.
∴S≠1.
(3)如图2所示:连接DF交EG于点M,过点M作MN⊥y轴,垂足为N.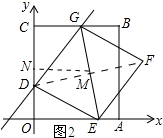
又∵四边形DEFG为菱形,
∴DM⊥GM,点M为DF的中点.
∵GD平分∠CGE,DM⊥GM,GC⊥OC,
∴MD=CD=4.
∵由(2)可知点F的坐标为4,点D的纵坐标为2,
∴点M的纵坐标为3.
∴ND=1.
在Rt△DNM中,MN=$\sqrt{D{M}^{2}-D{N}^{2}}$=$\sqrt{15}$.
∴点M的坐标为($\sqrt{15}$,3).
设直线DM的解析式为y=kx+2.将($\sqrt{15}$,3)代入得:$\sqrt{15}$k+2=3.
解得:k=$\frac{\sqrt{15}}{15}$.
∴设直线MG的解析式为y=$-\sqrt{15}$x+b.将($\sqrt{15}$,3)代入得:-15+b=3.
解得:b=18.
∴直线MG的解析式为y=-$\sqrt{15}$x+18.
将y=6代入得:$-\sqrt{15}x+18=6$.
解得:x=$\frac{4\sqrt{15}}{5}$.
∴点G的坐标为($\frac{4\sqrt{15}}{5}$,6).
将($\frac{4\sqrt{15}}{5}$,6)代入y=mx+2得:$\frac{4\sqrt{15}}{5}$m+2=6.
解得:m=$\frac{\sqrt{15}}{3}$.
故答案为:$\frac{\sqrt{15}}{3}$.
点评 本题考查的是一次函数的综合应用,解答本题主要应用了菱形的性质、全等三角形的性质和判定、待定系数法求一次函数的解析式、角平分线的性质,求得点M的坐标是解题的关键.


科目:初中数学 来源: 题型:选择题
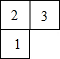 如图是由几个小立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,那么这个几何体的主视图是( )如图是由几个小立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,那么这个几何体的主视图是( )
如图是由几个小立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,那么这个几何体的主视图是( )如图是由几个小立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,那么这个几何体的主视图是( )| A. |  | B. | 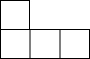 | C. | 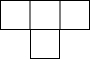 | D. | 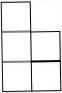 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
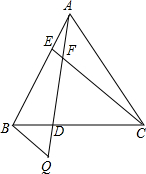 如图,点D,E分别在等边△ABC的边BC,AB上,且AE=BD,连接AD,CE交于点F,过点B作BQ∥CE交AD延长线于点Q.
如图,点D,E分别在等边△ABC的边BC,AB上,且AE=BD,连接AD,CE交于点F,过点B作BQ∥CE交AD延长线于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ②③④ | C. | ③④ | D. | ①③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com