
【题目】如图,在![]() ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.
ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.
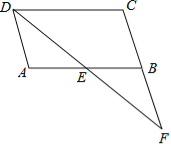
(1)求证:△ADE≌△BFE;
(2)若DF平分∠ADC,连接CE.试判断CE和DF的位置关系,并说明理由.
【答案】(1)由全等三角形的判定定理AAS证得结论。
(2)由(1)中全等三角形的对应边相等推知点E是边DF的中点,∠1=∠2;根据角平分线的性质、等量代换以及等角对等边证得DC=FC,则由等腰三角形的“三合一”的性质推知CE⊥DF。
【解析】
(1)由全等三角形的判定定理AAS证得结论。
(2)由(1)中全等三角形的对应边相等推知点E是边DF的中点,∠1=∠2;根据角平分线的性质、等量代换以及等角对等边证得DC=FC,则由等腰三角形的“三合一”的性质推知CE⊥DF。
解:(1)证明:如图,∵四边形ABCD是平行四边形,∴AD∥BC。

又∵点F在CB的延长线上,∴AD∥CF。∴∠1=∠2。
∵点E是AB边的中点,∴AE=BE,
∵在△ADE与△BFE中,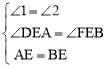 ,
,
∴△ADE≌△BFE(AAS)。
(2)CE⊥DF。理由如下:
如图,连接CE,
由(1)知,△ADE≌△BFE,
∴DE=FE,即点E是DF的中点,∠1=∠2。
∵DF平分∠ADC,∴∠1=∠3。∴∠3=∠2。
∴CD=CF。∴CE⊥DF。


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
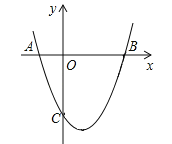
【题目】如图,抛物线与x轴的交点分别为A、B,与y轴的负半轴交于点C.已知抛物线的顶点坐标为(1,﹣4),点B的坐标(3,0).
(1)求该抛物线的解析式.
(2)在该函数图象上能否找到一点P,使PO=PC?若能,请求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
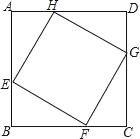
【题目】如图,在正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边上的动点,且AE=BF=CG=DH.
(1)求证:△AEH≌△CGF;
(2)在点E、F、G、H运动过程中,判断直线EG是否经过某一个定点,如果是,请证明你的结论;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,∠CAB=30°,DE⊥AC于E,且AE=CE,若DE=5,EB=12,求四边形ABCD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
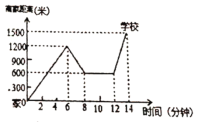
【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时间,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是 米,小明在书店停留了 分钟
(2)本次上学途中,小明一共行驶了 米,一共用了 分钟.
(3)我们认为骑单车的速度超过300米分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是 ( )

A. ![]() B. 2
B. 2![]() C. 3 D. 2
C. 3 D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
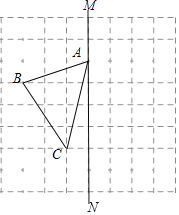
【题目】如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上)
(1)△ABC的面积为 ;
(2)在图中作出△ABC关于直线MN的对称图形△A'B'C';
(3)在MN上找一点P,使得PB+PC的距离最短,这个最短距离为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
(1)求出A、B、C三点的坐标和抛物线的对称轴;
(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m;
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?
②设△BCF的面积为S,求S与m的函数关系式,S是否有最大值?如有,请求出最大值,没有请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com