
 已知P为正方形ABCD内一点.△BPC为等边三角形.BD交PC于点E,若AB=2.则EC=( )
已知P为正方形ABCD内一点.△BPC为等边三角形.BD交PC于点E,若AB=2.则EC=( )| A. | 2$\sqrt{3}$+1 | B. | 2$\sqrt{3}$-2 | C. | 1.5 | D. | $\frac{5}{3}$ |
分析 作EH⊥CD于H.设DH=EH=a,则CH=$\sqrt{3}$a,EC=2a,根据CD=2列出方程求出a即可解决问题.
解答 解:作EH⊥CD于H.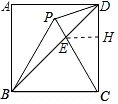
∵四边形ABCD是正方形,
∴∠BDC=45°,∠BCD=90°,AB=CD=2,
∴DH=EH,设DH=EH=a,
∵△PBC是等边三角形,
∴∠PCB=60°,
在Rt△ECH中,CH=$\frac{EH}{tan30°}$=$\sqrt{3}$a,
∴a+$\sqrt{3}$a=2,
∴a=($\sqrt{3}$-1),
∴EC=2EH=2a=2$\sqrt{3}$-2.
故选B
点评 本题考查正方形的性质、等边三角形的性质.等腰直角三角形的性质,直角三角形30度角性质等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
 如图,有以下四个条件:①∠B+∠BCD=180°,②∠3=∠4,③∠1=∠2,④∠B=∠5.其中能判定AB∥CD的条件的有①③④ (填序号)
如图,有以下四个条件:①∠B+∠BCD=180°,②∠3=∠4,③∠1=∠2,④∠B=∠5.其中能判定AB∥CD的条件的有①③④ (填序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=-3,b=2 | B. | a=3,b=2 | C. | a=-3,b=-2 | D. | a=3,b=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知AM为⊙O的直径,直线BC经过点M,且AB=AC,∠BAM=∠CAM,线段AB和AC分别交⊙O于点D、E,∠BMD=40°,则∠EOM=80°.
如图,已知AM为⊙O的直径,直线BC经过点M,且AB=AC,∠BAM=∠CAM,线段AB和AC分别交⊙O于点D、E,∠BMD=40°,则∠EOM=80°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 垂心 | B. | 重心 | C. | 内心 | D. | 外心 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com