
【题目】已知:如图,D是AC上一点,BE∥AC,BE=AD,AE分别交BD、BC于点F、G,且∠1=∠2.
(1)填空:图中与△BEF全等的三角形是______,与△BEF相似的三角形是_____(不再添加任何辅助线);
(2)对(1)中的两个结论选择其中一个给予证明.
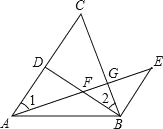
【答案】(1)△BEF≌△DAF;△BEF∽△GBF;(2)证明见解析.
【解析】
(1)结合图形,根据全等三角形的判定即可得解;根据相似三角形的判定,结合图形找出与△BEF能够有两组对应角相等的三角形即可;
(2)根据两直线平行,内错角相等可得∠1=∠E,然后利用“角角边”证明△BEF和△DAF全等;根据∠1=∠2可得∠2=∠E,又∠E为公共角,可以证明△BEF和△GBF相似.
(1)解:△BEF≌△DAF,△BEF∽△GBF;
(2)证明:∵BE∥AC,
∴∠1=∠E,
在△BEF和△DAF中,
∵ ,
,
∴△BEF≌△DAF(AAS);
∵BE∥AC,
∴∠1=∠E,
∵∠1=∠2,
∴∠2=∠E,
又∵∠F为公共角,
∴△BEF∽△GBF.


科目:初中数学 来源: 题型:
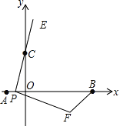
【题目】如图,在平面直角坐标系中,已知点A、B、C的坐标分别为(﹣1,0),(5,0),(0,2).若点P从A点出发,沿x轴正方向以每秒1个单位长度的速度向B点移动,连接PC并延长到点E,使CE=PC,将线段PE绕点P顺时针旋转90°得到线段PF,连接FB.若点P在移动的过程中,使△PBF成为直角三角形,则点F的坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阳光通过窗口照到教室内,竖直窗框在地面上留下2.1 m长的影子如图所示,已知窗框的影子DE的点E到窗下墙脚的距离CE=3.9 m,窗口底边离地面的距离BC=1.2 m,试求窗口的高度(即AB的值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标).
(1)求P点落在正方形ABCD面上(含正方形内部和边界)的概率.
(2)将正方形ABCD平移整数个单位,则是否存在一种平移,使点P落在正方形ABCD
面上的概率为0.75;若存在,指出其中的一种平移方式;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具商店对文具进行组合销售,甲种组合:2支红色圆珠笔,4支黑色圆珠笔;乙种组合:3支红色圆珠笔,8支黑色圆珠笔,1个笔记本;丙种组合:2支红色圆珠笔,6支黑色圆珠笔,1个笔记本.已知红色圆珠笔每支2元,黑色圆珠笔每支1.5元,笔记本每个10元.某个周末销售这三种组合文具共485元,其中红色圆珠笔的销售额为116元,则笔记本的销售额为________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=![]() S△ABF,其中正确的结论有________个。
S△ABF,其中正确的结论有________个。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )

A. ①②③④ B. ②③ C. ①②④ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com