
| A. | csinA=a | B. | bcosB=c | C. | atanA=b | D. | ctanB=b |
分析 由于a2+b2=c2,根据勾股定理的逆定理得到△ABC是直角三角形,且∠C=90°,再根据锐角三角函数的定义即可得到正确选项.
解答 解:∵a2+b2=c2,
∴△ABC是直角三角形,且∠C=90°.
A、sinA=$\frac{a}{c}$,则csinA=a.故本选项正确;
B、cosB=$\frac{a}{c}$,则cosBc=a.故本选项错误;
C、tanA=$\frac{a}{b}$,则$\frac{a}{tanA}$=b.故本选项错误;
D、tanB=$\frac{b}{a}$,则atanB=b.故本选项错误.
故选:A.
点评 本题考查了锐角三角函数的定义和勾股定理的逆定理.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
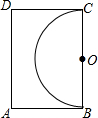 如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )| A. | 3m | B. | 5m | C. | 7m | D. | 9m |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com