
����Ŀ������ʱ���������뵽�ķ���δ������ģ����������һ�룬�����Ż��ⷨ��
�������
����x�ķ���a(x��m)2��b��0�Ľ���x1��1��x2����2��a��m��b��Ϊ������a��0������a(x��m��2)2��b��0�Ľ����� ��
�ⷨ̽��
��1��С����˼·��ͼ��ʾ�����㰴������˼·���������⣻
С����˼·
��1�� ��1����2���뵽��1�����������m��ֵ��
��2�� ��m��ֵ���뵽��1�����������![]() ��ֵ��
��ֵ��
��3�� ���2�����̣�
��2��С����ϸ�۲��������̣����ѵ�2������a(x��m��2)2��b��0�еġ�x��2��������1�������еġ�x������x��2����ֵΪ�� ���Ӷ����ؽ�������⣮
��������
��3��С����С������˼�����֣����÷��̽ṹ���ص㣬������㡰�����б�ʽ���������ɽ���������⣬��������˵�ķ�����ɽ��
��֪���� (a2��2b2)x2��(2b2��2c2)x��2c2��a2��0��������ȵ�ʵ����������a��b��c�ǡ�ABC���ߵij����жϡ�ABC����״��
���𰸡���1��x1����1��x2����4 ��2��1��2 ��3��ֱ��������
��������
��1�������������ô���ϵ������⼴��.
��2���Ѻ���һ�������е�x+2�������壬�൱��ǰ��һ�������е�x��⣮
��3���ȸ�����������ȵ�ʵ�������ٸ��ݸ���ϵ���Ĺ�ϵ�г����̣��ҵ�a��b��c�Ĺ�ϵ���Ӷ��ж������ε���״��
��1���⣺��x1��1��x2����2���뵽����a(x��m)2��b��0�У�
�� ��
��
�� m��1����(m��2)��
��� m��![]()
�� a(![]() ��1)2��b��0��
��1)2��b��0��
�� ��![]() ��
��![]()
��2�����̿ɱ���Ϊ(x��![]() ��2)2����
��2)2����![]() ��
��
��(x��![]() )2��
)2��![]() ��
��
��ã�x1����1��x2����4
��2������x�ķ���a��x+m��2+b=0�Ľ���x1=-2��x2=1����a��m��b��Ϊ������a��0����
��3���⣺�� (a2��2b2)��(2b2��2c2)��(2c2��a2)��0��
�� ���̱���һ����x��1
�� ���̵�����Ϊx1��x2��1��
�� x1��x2��1��![]() ��
��
�� a2��b2��c2��
�� ��ABC��һ��ֱ��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����λͬѧ5����ѧѡ�����ijɼ�ͳ�����±�������5�ο��Ե��ܳɼ���ͬ����ͬѧ������������⣺
��1 �� | ��2 �� | �� 3�� | �� 4�� | ��5 �� | |
�׳ɼ� | 90 | 40 | 70 | 40 | 60 |
�ҳɼ� | 70 | 50 | 70 |
| 70 |
��1��ͳ�Ʊ��У���![]() ��ֵ����ͬѧ�ɼ��ļ���Ϊ���٣�
��ֵ����ͬѧ�ɼ��ļ���Ϊ���٣�
��2��Сӱ�����˼�ͬѧ�ijɼ�ƽ����Ϊ60��������![]() [(90��60)2+(40��60)2+(70��60)2+(40��60)2+(60��60)2]��360.
[(90��60)2+(40��60)2+(70��60)2+(40��60)2+(60��60)2]��360.
���������ͬѧ�ɼ���ƽ�����ͷ��
��3����ƽ�����ͷ���ĽǶȷ�����������λͬѧ˭�ijɼ����ȶ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������֪����
���е�����ֵ������ֱ��ƽ�еģ���ˣ�����������ֱ�����ߵ���Ŀ�ĵأ�ֻ�ܰ�ֱ�ǹ���ķ�ʽ���ߣ������սֵ��Ĵ�ֱ��ƽ�з�����ƽ��ֱ������ϵxOy��������A(![]() ��
��![]() )��B(
)��B(![]() ��
��![]() )�������·�ʽ�����������룺d(A��B)��
)�������·�ʽ�����������룺d(A��B)��![]() ��
��![]() ��
��
����ѧ���⣩��
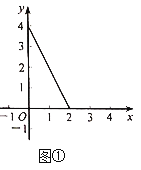
��1������֪��A(��2��1)����d(O��A)�� ���ں���![]() (0��x��2)��ͼ����ͼ����ʾ��B��ͼ����һ�㣬d(O��B)��3�����B�������� ��
(0��x��2)��ͼ����ͼ����ʾ��B��ͼ����һ�㣬d(O��B)��3�����B�������� ��
��2������![]() (x��0)��ͼ����ͼ����ʾ����֤���ú�����ͼ���ϲ����ڵ�C��ʹd(O��C)��3��
(x��0)��ͼ����ͼ����ʾ����֤���ú�����ͼ���ϲ����ڵ�C��ʹd(O��C)��3��

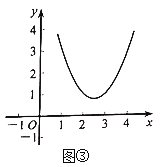
��3������![]() (x��0)��ͼ����ͼ����ʾ��D��ͼ����һ�㣬��d(O��D)����Сֵ����Ӧ�ĵ�D�����꣮
(x��0)��ͼ����ͼ����ʾ��D��ͼ����һ�㣬��d(O��D)����Сֵ����Ӧ�ĵ�D�����꣮
������������
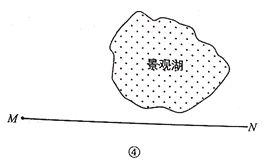
��4��ij��Ҫ��һ��ͨ�����ۺ��ĵ�·����ͼ�ܣ���·��MΪ��㣬����MN����ij�������ڸô���һ��ֱ������ֱ�ߵ����ߣ��������ʹ��·��̣���Ҫ�����ʵ���ƽ��ֱ������ϵ������ʾ��ͼ����Ҫ˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O�İ뾶Ϊ4��AB��AC�ǡ�O���������ң�AB��![]() ����O��AC�ľ���Ϊ
����O��AC�ľ���Ϊ![]() ���������BAC�Ķ���.
���������BAC�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η��� kx2��(2k��1)x��k��2��0��
��1�����÷�������������ȵ�ʵ��������k��ȡֵ��Χ��
��2�����÷��̵�����x1��x2����![]() ����3����k��ֵ��
����3����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
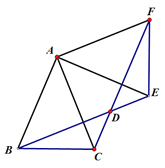
����Ŀ����ͼ,����ABC��,AB=AC=2,��BAC=45��,��AEF������ABC�Ƶ�A����ʱ�뷽����ת�õ���,����BE��CF�ཻ�ڵ�D.
(1)��֤: BE=CF;
(2)��̽����ת�ǵ��ڶ��ٶ�ʱ,�ı���ABDFΪ����,֤����Ľ���;
(3)��(2)��������,��CD�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������D��E�ֱ�����ABC�еı�AB��AC�ϣ���ô�����ж�DE��BC�ı���ʽ�ǣ�������
A. AD��DB��AE��EC B. DE��BC��AD��AB
C. BD��AB��CE��AC D. AB��AC��AD��AE
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
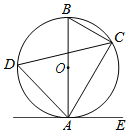
����Ŀ����ͼ����֪AB�ǡ�O��ֱ������C��D�ڡ�O�ϣ���E�ڡ�O�⣬��EAC����D��
��1����֤��AE�ǡ�O�����ߣ�
��2����BC��2����D��60��ʱ�����ӻ�AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+cͼ���һ���֣�ͼ�����A����3��0�����Գ���Ϊx=��1�������ĸ����ۣ���b2��4ac����2a+b=0����3a+c=0����a+b+c=0��������ȷ���۵ĸ����ǣ�������

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com