
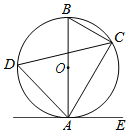
【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D.
(1)求证:AE是⊙O的切线;
(2)若BC=2,∠D=60°时,求劣弧AC的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由AB是⊙O的直径,根据半圆(或直径)所对的圆周角是直角,即可得∠ACB=90°,又由∠BAC=30°,易求得∠BAE=90°,则可得AE是⊙O的切线;
(2)首先连接OC,易得△OBC是等边三角形,则可得∠AOC=120°,由弧长公式,即可求得劣弧AC的长.
解:(1)∵∠ABC与∠D都是弧AC所对的圆周角,
∴∠ABC=∠D,
∵AB是⊙O的直径,
∴∠ACB=90°.
∴∠BAC=30°,
∴∠BAE=∠BAC+∠EAC=30°+60°=90°,
即BA⊥AE,
∴AE是⊙O的切线;
(2)如图,连接OC,
∵∠ABC=∠D=60°,
∴∠AOC=120°,
∴劣弧AC的长为![]() =
=![]() .
.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE=![]() ,∠DPA=45°.
,∠DPA=45°.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解题时,最容易想到的方法未必是最简单的,你可以再想一想,尽量优化解法.
例题呈现
关于x的方程a(x+m)2+b=0的解是x1=1,x2=-2(a、m、b均为常数,a≠0),则方程a(x+m+2)2+b=0的解是 .
解法探讨
(1)小明的思路如图所示,请你按照他的思路解决这个问题;
小明的思路
第1步 把1、-2代入到第1个方程中求出m的值;
第2步 把m的值代入到第1个方程中求出![]() 的值;
的值;
第3步 解第2个方程.
(2)小红仔细观察两个方程,她把第2个方程a(x+m+2)2+b=0中的“x+2”看作第1个方程中的“x”,则“x+2”的值为 ,从而更简单地解决了问题.
策略运用
(3)小明和小红认真思考后发现,利用方程结构的特点,无需计算“根的判别式”就能轻松解决以下问题,请用他们说的方法完成解答.
已知方程 (a2-2b2)x2+(2b2-2c2)x+2c2-a2=0有两个相等的实数根,其中a、b、c是△ABC三边的长,判断△ABC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 中(
中(![]() ,
,![]() 是常数)的自变量
是常数)的自变量![]() 与函数值
与函数值![]() 的部分对应值如下表:
的部分对应值如下表:
| …… |
| 0 | 1 | 2 | 3 | 4 | …… |
| …… | 10 | 5 | 2 | 1 | 2 | 5 | …… |
下列结论正确的是:
A.当![]() 时,
时,![]() 有最大值1
有最大值1
B.当![]() 时,
时,![]() 随
随![]() 的增大而增大
的增大而增大
C.点![]() 在该函数的图像上
在该函数的图像上
D.若![]() ,
,![]() 两点都在该函数的图象上,则当
两点都在该函数的图象上,则当![]() 时,
时,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目:初中数学 来源: 题型:
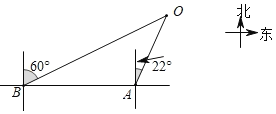
【题目】2019年4月23日是中国人民解放军海军成立70周年纪念日,届时将在青岛举行盛大的多国海军庆祝活动.为此我国海军进行了多次军事演习.如图,在某次军事演习时,舰艇A发现在他北偏东22°方向上有不明敌舰在指挥中心O附近徘徊,快速报告给指挥中心,此时在舰艇A正西方向50海里处的舰艇B接到返回指挥中心的行动指令,舰艇B迅速赶往在他北偏东60°方向的指挥中心处,舰艇B的速度是80海里/小时,请根据以上信息,求舰艇B到达指挥中心O的时间.(结果精确到0.1小时,参考数据:(sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,矩形ABCD的对角线AC与BD相交于点O,点O关于直线AD的对称点是E,连接AE、DE.
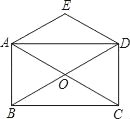
(1)试判断四边形AODE的形状,不必说明理由;
(2)请你连接EB、EC,并证明EB=EC.
查看答案和解析>>
科目:初中数学 来源: 题型:
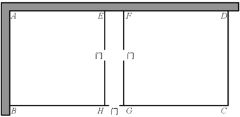
【题目】某农场要建一个饲养场(矩形ABCD)两面靠现有墙(AD位置的墙最大可用长度为27米,AB位置的墙最大可用长度为15米),另两边用木栏围成,中间也用木栏隔开,分成两个场地及一处通道,并在如图所示的三处各留1米宽的门(不用木栏)。建成后木栏总长45米。设饲养场(矩形ABCD)的一边AB长为x米.
(1)饲养场另一边BC= 米(用含x的代数式表示).
(2)若饲养场的面积为180平方米,求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com