练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知抛物线y=x2﹣2kx+3k+4．

    （1）抛物线经过原点时，求k的值.

    （2）顶点在x轴上时，求k的值；

    （3）顶点在y轴上时，求k的值；

    【答案】（1）k=﹣；（2）k=4或k=﹣1；（3）k=0

    【解析】

    （1）把（0,0）代入解析式即可求解；

    （2）根据顶点在x轴上得到b2﹣4ac=0，代入即可求解；

    （3）根据顶点在y轴上得到﹣2k=0，

    （1）∵抛物线y=x2﹣2kx+3k+4经过原点，把（0,0）代入得3k+4=0，

    解得：k=﹣ ．

    （2）∵抛物线y=x2﹣2kx+3k+4顶点在x轴上，

    ∴b2﹣4ac=0，

    ∴（﹣2k）2﹣4×1×（3k+4）=0，

    解得：k=4或k=﹣1；

    （3）∵抛物线y=x2﹣2kx+3k+4顶点在y轴上，

    ∴﹣2k=0，

    解得：k=0

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读下文并解答问题：

    （1）小丽袋子中卡片上分标有1，2，3，4；小兵袋子中卡片上分别标有1，2，3．分别用a、b表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字，请用树状图法或列表法写出（a，b）的所有取值情况；

    （2）求a＞b概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商品的进价为每件40元，售价每件不低于60元且每件不高于80元.当售价为每件60元是，每个月可卖出100件；如果每件商品的售价每上涨1元，则每个月少卖2件.设每件商品的售价为元（为正整数），每个月的销售利润为元.

    （1）求与的函数关系式并直接写出自变量的取值范围；

    （2）每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？

    （3）当每件商品定价为多少元使得每个月的利润恰为2250元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知在△ABC中，AB=AC，AD⊥BC，垂足为点D，以AD为对角线作正方形AEDF，DE交AB于点M，DF交AC于点N，连结EF，EF分别交AB、AD、AC于点G、点O、点H.

    （1）求证：EG=HF；

    （2）当∠BAC=60°时，求的值；

    （3）设,△AEH和四边形EDNH的面积分别为S1和S2，求的最大值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】以下说法合理的是（　　）

    A. 小明做了3次掷图钉的实验，发现2次钉尖朝上，由此他说钉尖朝上的概率是

    B. 某彩票的中奖概率是5%，那么买100张彩票一定有5张中奖

    C. 某射击运动员射击一次只有两种可能的结果：中靶与不中靶，所以他击中靶的概率是

    D. 小明做了3次掷均匀硬币的实验，其中有一次正面朝上，2次正面朝下，他认为再掷一次，正面朝上的概率还是

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的方程x2﹣（2m﹣1）x+m2+1＝0有两个不相等实数根x1，x2

    （1）求实数m的取值范围；

    （2）若x12+x22＝x1x2+3时，求实数m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

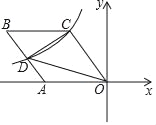
    【题目】如图，菱形OABC的一边OA在x轴的负半轴上，O是坐标原点，tan∠AOC=，反比例函数y=﹣的图象经过点C，与AB交与点D，则△COD的面积的值等于_____；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

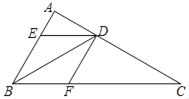
    【题目】如图，BD是△ABC的角平分线，过点D作DE∥BC交AB于点E，DF∥AB交BC于点F．

    （1）求证：四边形BEDF为菱形；

    （2）如果∠A＝90°，∠C＝30°，BD＝6，求菱形BEDF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将两块大小相同的含30°角的直角三角板(=30°)按图1的方式放置，固定三角板ABC然后将三角板ABC绕直角顶点C顺时针方向旋转（旋转角小于90°）至图2所示的位置，AB与AC交于点E，AC与AB交于点F，AB与AB交于点O.

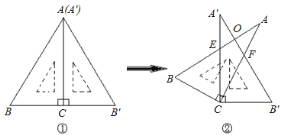
    (1)求证：；

    (2)当旋转角等于30°时，AB与AB垂直吗？请说明理由。

    查看答案和解析>>

    同步练习册答案