
【题目】已知:如图,矩形ABCD的对角线AC与BD相交于点O,点O关于直线AD的对称点是E,连接AE、DE.
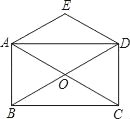
(1)试判断四边形AODE的形状,不必说明理由;
(2)请你连接EB、EC,并证明EB=EC.
【答案】(1) 四边形AODE是菱形.理由见解析;(2)见解析.
【解析】
(1)利用对称的性质,又因为四边形ABCD是矩形,两个结论联合起来,可知四边形AODE是菱形;
(2)先证出∠EAB=∠EDC,再证明△EAB≌△EDC,从而得出EB=EC.
(1)四边形AODE是菱形.理由如下:
∵点O和点E关于直线AD对称,
∴△AOD≌△AED;
∴OA=AE OD=DE;
∵由矩形ABCD,
∴OA=OD;
∴OA=OD=DE=EA;
∴四边形AODE是菱形.
(2)连接EB、EC,如图,

∵四边形AODE是菱形,
∴AE=ED;
∴∠EAD=∠EDA;
∵四边形ABCD是矩形,
∴AB=CD,∠BAD=∠CDA=90°;
∴∠EAD+∠BAD=∠EDA+∠CDA;
∴∠EAB=∠EDC;
∴△EAB≌△EDC;
∴EB=EC.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
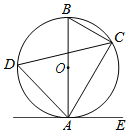
【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D.
(1)求证:AE是⊙O的切线;
(2)若BC=2,∠D=60°时,求劣弧AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:

(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
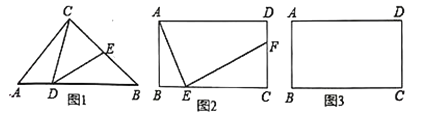
【题目】(1)如图1所示,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在斜边
在斜边![]() 上,点
上,点![]() 在直角边
在直角边![]() 上,若
上,若![]() ,求证:
,求证:![]() .
.
(2)如图2所示,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() (或
(或![]() 的延长线)于点
的延长线)于点![]() .
.
①若![]() ,求
,求![]() 的长;
的长;
②若点![]() 恰好与点
恰好与点![]() 重合,请在备用图上画出图形,并求
重合,请在备用图上画出图形,并求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac;②2a+b=0;③3a+c=0;④a+b+c=0.其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+1的顶点为D,与x轴正半轴交于A、B两点,A在B左,与y轴正半轴交于点C,当△ABD和△OBC均为等腰直角三角形(O为坐标原点)时,b的值为( )

A. 2 B. ﹣2或﹣4 C. ﹣2 D. ﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
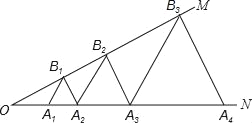
【题目】如图,已知:∠MON=30°,点A1、A2、A3在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com