
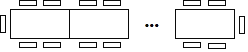
【题目】一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图所示的方式进行拼接.
(1)若把4张这样的餐桌拼接起来,四周可坐 人;
(2)若把n张这样的餐桌拼接起来,四周可坐 人;
(3)若把9张这样的餐桌拼接起来,四周可坐 人;
(4)若用餐的人数有50人,则这样的餐桌需要多少张?
【答案】(1)18;(2)(4n+2);(3)38;(4)这样的餐桌需要12张
【解析】
(1)根据图形的变化可知4张这样的餐桌拼接起来,四周可坐4×4+2=18人;
(2)把n张这样的餐桌拼接起来,四周可坐4n+2人;
(3)把9张这样的餐桌拼接起来,四周可坐4×9+2=38人;
(4)用餐的人数有50人,则4n+2=50,n=12,即可计算这样的餐桌需要多少张.
解:(1)4张长方形餐桌拼接起来四周可坐4×4+2=18(人),
故答案为18;
(2)n张长方形餐桌拼接起来四周可坐(4n+2)人,
故答案为(4n+2);
(3)9张长方形餐桌拼接起来四周可坐38人,
故答案为38;
(3)若用餐的人数有50人,则4n+2=50,解得n=12.
答:这样的餐桌需要12张.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】为解方程(x2﹣1)2﹣5(x2﹣1)+4=0,我们可以将x2﹣1视为一个整体,然后设x2﹣1=y,则
(x2﹣1)=y2,原方程化为y2﹣5y+4=0.①
解得y1=1,y2=4
当y=1时,x2﹣1=1.∴x2=2.∴x=±![]() ;
;
当y=4时,x2﹣1=4,∴x2=5,∴x=±![]() .
.
∴原方程的解为x1=![]() ,x2=﹣
,x2=﹣![]() ,x3=
,x3=![]() ,x4=﹣
,x4=﹣![]()
解答问题:
(1)填空:在由原方程得到方程①的过程中,利用 法达到了降次的目的,体现了 的数学思想.
(2)解方程:x4﹣x2﹣6=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1和图2,半圆O的直径AB=4,点P(不与点A,B重合)为半圆上一点,将图形沿着BP折叠,分别得到点A,O的对称点A′,O′,设∠ABP=α.
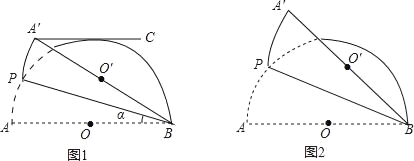
(1)如图1,当α=22.5°时,过点A′作A′C∥AB,判断A′C与半圆O的位置关系,并说明理由.
(2)如图2,当α= 时,点O′落在![]() 上.当α= 时,BA′与半圆O相切.
上.当α= 时,BA′与半圆O相切.
(3)当线段B O′与半圆O只有一个公共点B时,α的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
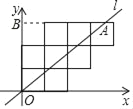
【题目】如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线l将图形分成面积相等的两部分,则将直线l向右平移3个单位长度后所得直线l′的函数解析式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的顶点为B(1,﹣3),与x轴的一个交点A在(2,0)和(3,0)之间,下列结论中:①bc>0;②2a+b=0;③a﹣b+c>0;④a﹣c=3,正确的有( )个
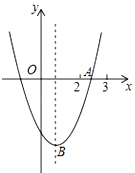
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知:![]() ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么![]() ABCD的周长是多少?
ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
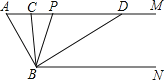
【题目】综合与探究:如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与点A不重合).BC,BD别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠ABN、∠CBD的度数;根据下列求解过程填空.
解:∵AM∥BN,
∴∠ABN+∠A=180°
∵∠A=60°,
∴∠ABN= ,
∴∠ABP+∠PBN=120°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP、∠PBN= ,( )
∴2∠CBP+2∠DBP=120°,
∴∠CBD=∠CBP+∠DBP= .
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,直接写出∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
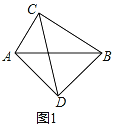
【题目】问题背景:如图(1)在四边形ABCD中,∠ACB=∠ADB=90°,AD=BD,探究线段AC、BC、CD之间的数量关系.小明探究此问题的思路是:将△BCD绕点D逆时针旋转90°到△AED处,点B、C分别落在点A、E处(如图(2)),易证点C、A、E在同一条直线上,并且△CDE是等腰直角三角形,所以CE=![]() CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC=![]() CD.
CD.
简单应用:
(1)在图(1)中,若AC=![]() ,BC=2
,BC=2![]() ,求CD的长;
,求CD的长;
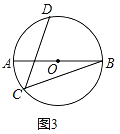
(2)如图(3)AB是⊙O的直径,点C、D在⊙O上,AD=BD,若AB=13,BC=12,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
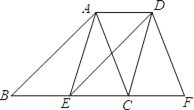
【题目】如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.
(1)求证:△ABC≌△DEF;
(2)求证:四边形ACFD为平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com