
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点A在x轴负半轴上,顶点B在x轴正半轴上.若抛物线p=ax2-10ax+8(a>0)经过点C、D,则点B的坐标为________.
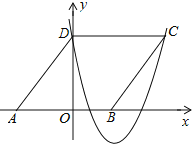
【答案】(4,0)
【解析】
根据抛物线p=ax210ax+8(a>0)经过点C、D和二次函数图象具有对称性,可以求得该抛物线顶点的横坐标和CD的长,然后根据菱形的性质和勾股定理可以求得AO的长,从而可以求得OB的长,进而写出点B的坐标.
解:∵抛物线p=ax210ax+8=a(x5)225a+8,
∴该抛物线的顶点的横坐标是x=5,当x=0时,y=8,
∴点D的坐标为:(0,8),
∴OD=8,
∵抛物线p=ax210ax+8(a>0)经过点C、D,CD∥AB∥x轴,
∴CD=5×2=10,
∴AD=10,
∵∠AOD=90°,OD=8,AD=10,
∴AO=![]() ,
,
∵AB=10,
∴OB=10AO=106=4,
∴点B的坐标为(4,0),
故答案为:(4,0)


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(x-2)(x-3)=m2,m为实数.
(1)求证:无论m为何值,方程总有两个不相等的实数根.
(2)m为何值时,方程有整数解.(直接写出三个,不需说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“朗读者”节目的影响下,某中学在暑期开展了“好书伴我成长”读书话动,并要求读书要细读,最少要读完2本书,最多不建议超过5本。初一年级5个班,共200名学生,李老师为了了解学生暑期在家的读书情况,给全班同学布置了一项调查作业:了解初一年级学生暑期读书情况.班中三位同学各自对初一年级读书情况进行了抽样调查,并将数据进行了整理,绘制的统计图表分别为表1、表2、表3.
表1:在初一年级随机选择5名学生暑期读书情况的统计表
阅读书数量(本) | 2 | 3 | 4 | 5 |
人数 | 2 | 1 | 1 | 1 |
表2:在初一年级“诵读班”班随机选取20名学生暑期读书情况的统计表
阅读书数量(本) | 2 | 3 | 4 | 5 |
人数 | 0 | 1 | 4 | 15 |
表3:在初一年级随机选取20名学生暑期读书情况的统计表
阅读书数量(本) | 2 | 3 | 4 | 5 |
人数 | 2 | 8 | 6 | 4 |
问题1:根据以上材料回答:三名同学中,哪一位同学的样本选取更合理,并简要说明其他两位同学选取样本的不足之处;
老师又对合理样本中的所有学生进行了“阅读动机”的调研,并制作成了如下统计图.
问题2:通过统计图的信息你认为“阅读动机”
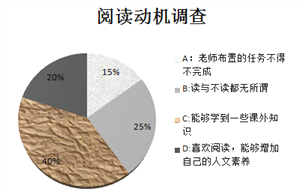
在“40%”的群体,暑期读几本书的可能性大,并说出你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
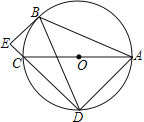
【题目】如图,⊙O是△ABC的外接圆,AC为直径,BD=BA,BE⊥DC交DC的延长线于点E
(1) 求证:BE是⊙O的切线
(2) 若EC=1,CD=3,求cos∠DBA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(1,2)为反比例函数![]() 图象上一点,
图象上一点,
(1) 将点A沿x轴正方向平移1个单位,对应点A′的坐标为___________
将比例函数![]() 图象沿x轴正方向平移1个单位,平移后的函数解析式为___________
图象沿x轴正方向平移1个单位,平移后的函数解析式为___________
将比例函数![]() 图象沿x轴正方向平移m个单位,平移后的函数解析式为___________
图象沿x轴正方向平移m个单位,平移后的函数解析式为___________
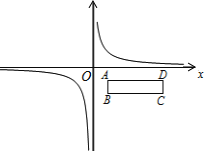
(2) 在平面直角坐标系中,矩形ABCD位置如图,其中A、B、C三点的坐标分别为A(1,-1)、B(1,-2)、C(4,-2).现将反比例函数![]() 图象沿x轴正方向平移,若平移速度为每秒1个单位长度
图象沿x轴正方向平移,若平移速度为每秒1个单位长度
① 设函数图象平移时间为t秒,求函数图象与矩形ABCD有公共点时t的取值范围;
② 在平移过程中,当函数图象与矩形ABCD有公共点时,则函数图象扫过的区域夹在直线AD、BC的图形面积为___________(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C、D、E在同一直线上,且AC=BD,E是线段BC的中点.
![]()
(1)点E是线段AD的中点吗?说明理由;
(2)当AD=10,AB=3时,求线段BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】食品厂从生产的袋装食品中抽出样品![]() 袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负来表示,记录如下表;
袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负来表示,记录如下表;
与标准质量的差值(单位:克) |
|
|
|
|
|
|
袋数 |
|
|
|
|
|
|
(1)这批样品的平均质量比标准质量是超过还是不足?平均每袋超过或不足多少克?
(2)若每袋标准质量为![]() 克,求抽样检测的样品总质量是多少?
克,求抽样检测的样品总质量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给下列证明过程填写理由.
如图,CD⊥AB于D,点F是BC上任意一点,EF⊥AB于E,∠1=∠2,求证:∠ACB=∠3.
请阅读下面解答过程,并补全所有内容.
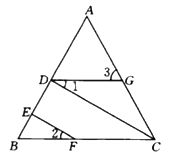
解:∵CD⊥AB,EF⊥AB(已知)
∴∠BEF=∠BDC=90°( )
∴EF∥DC( )
∴∠2=________( )
又∵∠2=∠1(已知)
∴∠1=_______(等量代换)
∴DG∥BC( )
∴∠3=________( )
查看答案和解析>>
科目:初中数学 来源: 题型:
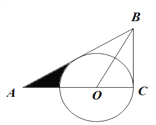
【题目】如图,△ABC中,∠C=90,∠ABC=2∠A,点O在AC上,OA=OB,以O为圆心,OC为半径作圆.
(1)求证:AB是⊙O的切线;
(2)若BC=3,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com