
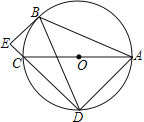
【题目】如图,⊙O是△ABC的外接圆,AC为直径,BD=BA,BE⊥DC交DC的延长线于点E
(1) 求证:BE是⊙O的切线
(2) 若EC=1,CD=3,求cos∠DBA
【答案】(1)证明见解析;(2)∠DBA![]()
【解析】(1)连接OB,OD,根据线段垂直平分线的判定,证得BF为线段AD的垂直平分线,再根据直径所对的圆周角为直角,得到∠ADC=90°,证得四边形BEDF是矩形,即∠EBF=90°,可得出结论.
(2)根据中点的性质求出OF的长,进而得到BF、DE、OB、OD的长,然后根据等角的三角函数求解即可.
证明:(1) 连接BO并延长交AD于F,连接OD
∵BD=BA,OA=OD
∴BF为线段AD的垂直平分线
∵AC为⊙O的直径
∴∠ADC=90°
∵BE⊥DC
∴四边形BEDF为矩形
∴∠EBF=90°
∴BE是⊙O的切线

(2) ∵O、F分别为AC、AD的中点
∴OF=![]() CD=
CD=![]()
∵BF=DE=1+3=4
∴OB=OD=![]()
∴cos∠DBA=cos∠DOF=


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
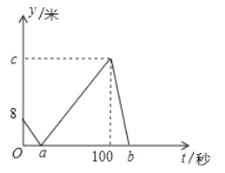
【题目】甲、乙两人在直线跑道上同起点同终点同方向匀速跑步500米,先到终点的人原地体息.已知甲先出发![]() ,在跑步过程中,甲、乙两人的距离
,在跑步过程中,甲、乙两人的距离![]() 与乙出发的时间
与乙出发的时间![]() 之间的关系如图所示,给出的下结论:①
之间的关系如图所示,给出的下结论:①![]() ,②
,②![]() ,③
,③![]() ,其中正确的是______.
,其中正确的是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,抛物线![]() 与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在![]() 轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点O为直线AB上一点,过点O作射线OC.将一直角三角板的直角顶点放在点O处.
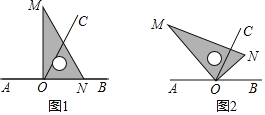
(1)如图1,若∠BOC=65°,将三角板MON的一边ON与射线OB重合时,则∠MOC= .
(2)如图2,若∠BOC=65°,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,则∠BON= .
(3)如图2,若∠BOC=α,仍然将三角板MON旋转到OC为∠MOB的角平分线的位置,求∠AOM.(写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=8,AC=6.点D在边AB上,AD=4.5.△ABC的角平分线AE交CD于点F.
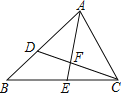
(1)求证:△ACD∽△ABC;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
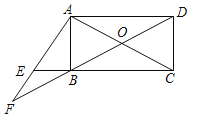
【题目】如图,平行四边形ABCD的对角线AC、BD交于点O,点E在边CB的延长线上,且∠EAC=90°,AE2=EBEC.
(1)求证:四边形ABCD是矩形;
(2)延长DB、AE交于点F,若AF=AC,求证:AE=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
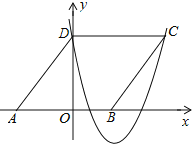
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点A在x轴负半轴上,顶点B在x轴正半轴上.若抛物线p=ax2-10ax+8(a>0)经过点C、D,则点B的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
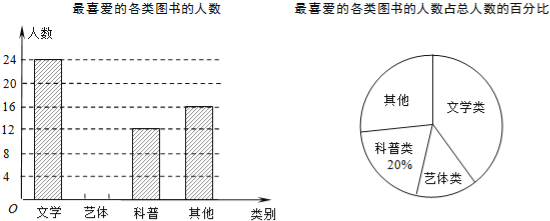
【题目】某校为了开阔学生的视野,积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答下列问题:
(1)求被调查的学生人数;
(2)补全条形统计图;
(3)已知该校有1200名学生,估计全校最喜爱文学类图书的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
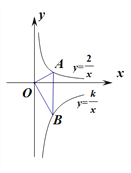
【题目】如图所示是一块含30°的直角三角板,直角顶点O位于坐标原点,斜边AB⊥x轴,顶点A在函数![]() (x>0)的图象上,顶点B在函数
(x>0)的图象上,顶点B在函数![]() (x>0)的图象上,∠ABO=30°,则k=_________.
(x>0)的图象上,∠ABO=30°,则k=_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com