
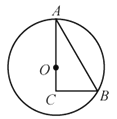
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1,以边AC上一点O为圆心,OA为半径的⊙O经过点B.
(1)求⊙O的半径;
(2)点P为![]() 中点,作PQ⊥AC,垂足为Q,求OQ的长;
中点,作PQ⊥AC,垂足为Q,求OQ的长;
(3)在(2)的条件下,连接PC,求tan∠PCA的值.
【答案】(1)⊙O的半径为![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)若连接OB,则△BCO是一个含30°角的直角三角形,△AOB是底角为30°的等腰三角形,可得∠OBC=30°,再根据特殊角的三角函数值求得OB;
(2) 连接OP,设AB与QP交于点M,根据题中条件证得∠QPO=∠A=30°,再根据特殊角的三角函数值求得OQ;
(3)可在Rt△PCQ中解决,分别计算出两条直角边,即可求出tan∠PCA的值.
(1)连接OB,如图
∵OA=OB,
∴∠ABO=∠A=30°,
∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∴∠OBC=30°,
在Rt△OBC中,![]() ,
,
即![]() ,
,
解得![]() ,
,
即⊙O的半径为![]() ;
;
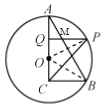
(2)连接OP,设AB与QP交于点M,
∵点P为![]() 的中点,
的中点,
∴OP⊥AB,
∴∠QPO+∠PMB=90°,
∵PQ⊥AC,
∴∠A+∠AMQ=90°,
又∵∠AMQ=∠PMB,
∴∠QPO=∠A=30°,
在Rt△OPQ中,![]() ,
,
即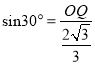 ,
,
∴![]()
(3)在Rt△OBC中,
∵![]() ,∠OBC=30°,∠ACB=90°
,∠OBC=30°,∠ACB=90°
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
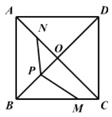
【题目】如图,在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中点,点M在BC边上,且BM=6. P为对角线BD上一点,则PM—PN的最大值为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
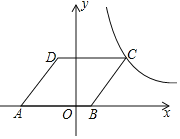
【题目】如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上,点A坐标为(-4,0),点D的坐标为(-1,4),反比例函数![]() 的图象恰好经过点C,则k的值为______.
的图象恰好经过点C,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是王阿姨晚饭后步行的路程s(单位:m)与时间t(单位:min)的函数图象,其中曲线段AB是以B为顶点的抛物线一部分.下列说法不正确的是( )
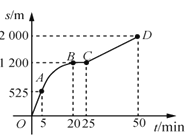
A.25min~50min,王阿姨步行的路程为800m
B.线段CD的函数解析式为![]()
C.5min~20min,王阿姨步行速度由慢到快
D.曲线段AB的函数解析式为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,则下列结论:①ac>0;②a﹣b+c<0;③当x<0时,y<0;④方程ax2+bx+c=0(a≠0)有两个大于﹣1的实数根.其中正确的结论有( )
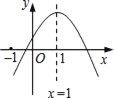
A. ①③ B. ②③ C. ①④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要在一块长52m,宽48m的矩形绿地上,修建同样宽的两条互相垂直的甬路.下面分别是小亮和小颖的设计方案.
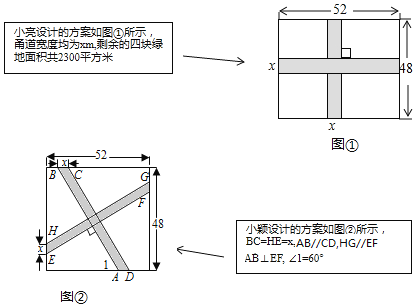
(1)求小亮设计方案中甬路的宽度x;
(2)求小颖设计方案中四块绿地的总面积(友情提示:小颖设计方案中的与小亮设计方案中的取值相同)
查看答案和解析>>
科目:初中数学 来源: 题型:
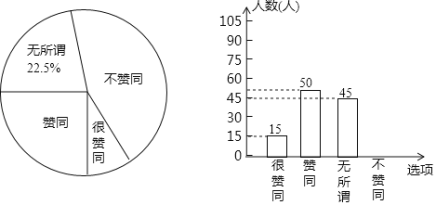
【题目】某校调查了若干名家长对“初中生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图,根据图中提供的信息,完成以下问题:
(1)本次共调查了 名家长,扇形统计图中“很赞同”所对应的圆心角度数是 度,并补全条形统计图.
(2)该校共有3600名家长,通过计算估计其中“不赞同”的家长有多少名?
(3)从“不赞同”的五位家长中(两女三男),随机选取两位家长对全校家长进行“学生使用手机危害性”的专题讲座,请用树状图或列表法求出选中“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
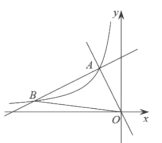
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 和
和![]() 的图象相交于点
的图象相交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(1)求反比例函数的表达式;
(2)设一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的另一个交点为
的图象的另一个交点为![]() ,连接
,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com