
【题目】如图,已知菱形![]() ,
,![]() ,
,![]() ,E为
,E为![]() 中点,P为对角线
中点,P为对角线![]() 上一点,则
上一点,则![]() 的最小值等于( )
的最小值等于( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
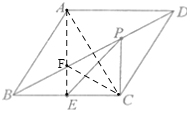
连接AC、AE,AE交BD于F,连接FC,由菱形的性质可得BD垂直平分AC,根据垂直平分线的性质可知AF=CF,FC+FE=AE,根据两点之间,线段最短可知,P点运动到F时,PE+PC的值最小,由∠BAD=120°可得∠ABC=60°,根据菱形的性质可得△ABC是等边三角形,根据等边三角形的性质求出AE的长即可.
连接AC、AE,AE交BD于F,连接FC,
∵ABCD是菱形,
∴BD垂直平分AC,
∴AF=FC,
∴FC+FE=AE,
∵两点之间,线段最短,
∴P点运动到F时,PE+PC的值最小,最小值为AE的长,
∵∠BAD=120°,
∴∠ABC=60°,
∵AB=BC,
∴△ABC是等边三角形,
∵E为BC中点,
∴AE⊥BC,BE=![]() BE=2,
BE=2,
∴AE=![]() =
=![]() =2
=2![]() .
.
故选B.


科目:初中数学 来源: 题型:
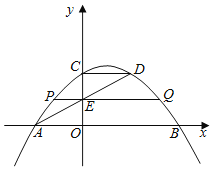
【题目】如图,抛物线![]() 与x轴相交于
与x轴相交于![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 在抛物线上,且
在抛物线上,且![]() .
.![]() 与
与![]() 轴相交于点
轴相交于点![]() ,过点
,过点![]() 的直线
的直线![]() 平行于
平行于![]() 轴,与拋物线相交于
轴,与拋物线相交于![]() 两点,则线段
两点,则线段![]() 的长为_____.
的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售部有营业员15人,该公司为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励,为了确定一个适当的月销售目标,公司有关部门统计了这15人某月的销售量,如下表所示:
月销售量/件数 | 1770 | 480 | 220 | 180 | 120 | 90 |
人数 | 1 | 1 | 3 | 3 | 3 | 4 |
(1)直接写出这15名营业员该月销售量数据的平均数、中位数、众数;
(2)如果想让一半左右的营业员都能达到月销售目标,你认为(1)中的平均数、中位数、众数中,哪个最适合作为月销售目标?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:①abc>0;②2a+b=0;③抛物线与x轴的另一个交点为(4,0);④c+a>b;⑤3a+c<0.其中正确的结论有______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年高一新生开始,某省全面启动高考综合改革,实行“3+1+2”的高考选考方案.“3”是指语文、数学、外语三科必考;“1”是指从物理、历史两科中任选一科参加选考,“2”是指从政治、化学、地理、生物四科中任选两科参加选考
(1)“1+2”的选考方案共有多少种?请直接写出所有可能的选法;(选法与顺序无关,例如:“物、政、化”与“物、化、政”属于同一种选法)
(2)高一学生小明和小杰将参加新高考,他们酷爱历史和生物,两人约定必选历史和生物.他们还需要从政治、化学、地理三科中选一科参考,若这三科被选中的机会均等,请用列表或画树状图的方法,求出他们恰好都选中政治的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组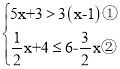 ,请结合题意填空,完成本题的解答,
,请结合题意填空,完成本题的解答,
I.解不等式①,得_________;
II.解不等式②,得________;
III.把不等式①和②的解集在数轴上表示出来:
![]()
IV.原不等式组的解集为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
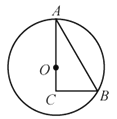
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1,以边AC上一点O为圆心,OA为半径的⊙O经过点B.
(1)求⊙O的半径;
(2)点P为![]() 中点,作PQ⊥AC,垂足为Q,求OQ的长;
中点,作PQ⊥AC,垂足为Q,求OQ的长;
(3)在(2)的条件下,连接PC,求tan∠PCA的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在-3、-2、-1、0、1、2,3,这七个数中,随机选取一个数,记为a,那么使得关于x的反比例函数![]() 的图像位于第一、三象限,且使得关于x的方程
的图像位于第一、三象限,且使得关于x的方程![]() 有整数解的概率为_____.
有整数解的概率为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com