
【题目】李老师准备购买若干个某种笔记本奖励学生,甲、乙两家商店都有足够数量的这种笔记本,其标价都是每个6元,甲商店的促销方案是:购买这种笔记本数量不超过5个时,原价销售;超过5个时,超过部分按原价的7折销售.乙商店的销售方案是:一律按标价的8折销售.
(1)若李老师要购买![]() 个这种笔记本,请用含
个这种笔记本,请用含![]() 的式子分别表示李老师到甲商店和乙商店购买全部这种笔记本所需的费用.
的式子分别表示李老师到甲商店和乙商店购买全部这种笔记本所需的费用.
(2)李老师购买多少个这种笔记本时,到甲、乙两家商店购买所需费用相同?
(3)若李老师需要20个这种笔记本,则到甲、乙哪家商店购买更优惠?
【答案】(1)甲:![]() ;乙:
;乙:![]() ;(2)李老师购买15个这种笔记本时,到甲、乙两家商店购买所需费用相同;(3)李老师到甲商店购买更优惠.
;(2)李老师购买15个这种笔记本时,到甲、乙两家商店购买所需费用相同;(3)李老师到甲商店购买更优惠.
【解析】
(1)根据甲、乙两文具店的销售方案,表示出李老师到两商店购买x(x>5)个笔记本所需的费用即可;
(2)当x>5时,由两店所需费用相同,可得出关于x的一元一次方程,解之即可得出结论;
(3)分别求出李老师到两商店购买笔记本所付费用,再进行比较即可.
解:(1)李老师到甲商店购买全部这种笔记本应付费:
![]() (元);
(元);
李老师到乙商店购买全部这种笔记本应付费:![]() (元).
(元).
(2)设李老师要购买![]() (由题可知
(由题可知![]() )个这种笔记本时,到甲、乙两家商店购买所需费用相同.
)个这种笔记本时,到甲、乙两家商店购买所需费用相同.
由题意,得![]() .
.
解得![]() .
.
答:李老师购买15个这种笔记本时,到甲、乙两家商店购买所需费用相同.
(3)李老师购买20个这种笔记本到甲商店应付费:![]() (元);
(元);
李老师购买20个这种笔记本到乙商店应付费:![]() (元).
(元).
因为93元![]() 元,所以李老师到甲商店购买更优惠.
元,所以李老师到甲商店购买更优惠.


科目:初中数学 来源: 题型:
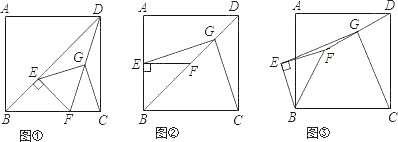
【题目】已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
(1)请问EG与CG存在怎样的数量关系,并证明你的结论;
(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?(请直接写出结果,不必写出理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
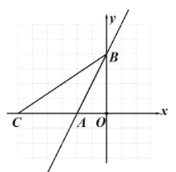
【题目】如图,一次函数y=2x+4的图象分别与x轴,y轴教育点A、点B、点C为x轴一动点。
(1)求A,B两点的坐标;
(2)当ΔABC的面积为6时,求点C的坐标;
(3)平面内是否存在一点D,使四边形ACDB使菱形,若存在,请直接写出点D的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
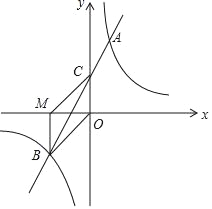
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2![]() ,点A的纵坐标为4.
,点A的纵坐标为4.
(1)求该反比例函数和一次函数的解析式;
(2)连接MC,求四边形MBOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°.把△ABC绕点A按顺时针方向旋转60°后得到△AB′C′,若AB=8,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是( )
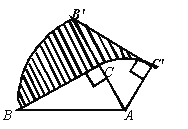
A. 8π B. 6π C. 4π D. 2π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某垃圾处理厂,对不可回收垃圾的处理费用为90元/吨,可回收垃圾的分拣处理费用也为90元/吨,分拣后再被相关企业回收,回收价格如下表:
垃圾种类 | 纸类 | 塑料类 | 金属类 | 玻璃类 |
回收单价(元/吨) | 500 | 800 | 500 | 200 |
据了解,可回收垃圾占垃圾总量的60%,现有![]() 三个小区12月份产生的垃圾总量分别为100吨,100吨和
三个小区12月份产生的垃圾总量分别为100吨,100吨和![]() 吨.
吨.
(1)已知![]() 小区金属类垃圾质量是塑料类的5倍,纸类垃圾质量是塑料类的2倍.设塑料类的质量为
小区金属类垃圾质量是塑料类的5倍,纸类垃圾质量是塑料类的2倍.设塑料类的质量为![]() 吨,则
吨,则![]() 小区可回收垃圾有______吨,其中玻璃类垃圾有_____吨(用含
小区可回收垃圾有______吨,其中玻璃类垃圾有_____吨(用含![]() 的代数式表示)
的代数式表示)
(2)![]() 小区纸类与金属类垃圾总量为35吨,当月可回收垃圾回收总金额扣除所有垃圾处理费后,收益16500元.求12月份该小区可回收垃圾中塑料类垃圾的质量.
小区纸类与金属类垃圾总量为35吨,当月可回收垃圾回收总金额扣除所有垃圾处理费后,收益16500元.求12月份该小区可回收垃圾中塑料类垃圾的质量.
(3)![]() 小区发现塑料类与玻璃类垃圾的回收总额恰好相等,所有可回收垃圾的回收总金额为12000元.设该小区塑料类垃圾质量为
小区发现塑料类与玻璃类垃圾的回收总额恰好相等,所有可回收垃圾的回收总金额为12000元.设该小区塑料类垃圾质量为![]() 吨,求
吨,求![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
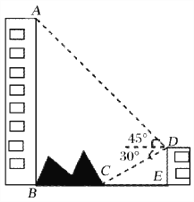
【题目】如图,大楼底右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上). 已知AB=80m,DE=10m,求障碍物B,C两点间的距离.(结果精确到0.1m)
(参考数据: ![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
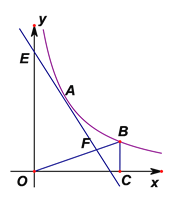
【题目】如图,直线![]() 与反比例函数
与反比例函数![]()
![]() 的图象只有一个交点
的图象只有一个交点![]() .
.
(1)求反比例函数的解析式;
(2)在函数![]() 的图象上取异于点
的图象上取异于点![]() 的一点
的一点![]() ,作
,作![]() 轴于点
轴于点![]() ,连接
,连接![]() 交直线于点
交直线于点![]() .设直线与
.设直线与![]() 轴交于点
轴交于点![]() ,若
,若![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍,求点
倍,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
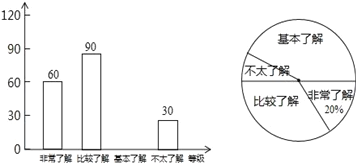
【题目】某校举行“足球在身边”的专题调查活动,采取随机抽样的方法进行问卷调查,调查结果划分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,并将调查结果绘制成两幅不完整的统计图(如图),请根据图中提供的信息,解答下列问题:
(1)被调查的学生共有___人.在扇形统计图中,表示“比较了解”的扇形的圆心角度数为___度
(2)请用列表法或树状分析从![]() 名男生和
名男生和![]() 名女生中随机抽取
名女生中随机抽取![]() 名学生参加“足球在身边”的知识竞赛,抽中
名学生参加“足球在身边”的知识竞赛,抽中![]() 男
男![]() 女的概率.
女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com